
[!] この記事は公開されてから1年以上経過しています。情報が古い可能性がありますので、ご注意ください。
はじめに
「ニューラルネットワークをスクラッチする」の第二回ということで、当記事では前回に引き続きライブラリを使用することなく1からニューラルネットワークをプログラミングするということをやっていきたいと思います(第一回の記事はこちら)。 今回まずは当ブログで利用する学習の種類を中心に「ニューラルネットワークが学習する仕組み」について説明した上で、実際のコーディングに入っていこうと思います。
学習の種類
それではAIの学習について簡単に説明したいと思います。AIの学習には大別すると「教師あり学習」と「教師なし学習」があります。
-
教師あり学習
AIが解決したい問題に明確な正解が存在し、入力データに対応する出力データ(正解)のペアを教師としてAIの出力結果と正解の誤差が小さくなるように学習していくようなイメージの学習になります。
例えば工場で「製品の画像」から不良品を分別したり、過去の「販売状況」「気温」「曜日」等のデータから来月の売上を予測するようなAIで用いられます。 -
教師なし学習
教師なし学習では、教師あり学習のように明確な正解となる教師データはありません。教師なし学習ではAIで解決したい問題に対して観測している状況や環境がより良い状態に遷移するような行動に対して報酬を設定し、その報酬が全体でより多くなるような行動を学んでいきます。
例えば囲碁や将棋をするAIや、より効率よく商品を配送するルートを探索したいといった最適化問題等を解くAI等ではこちらの学習を用いることが多いです。
当記事では前回のブログで記載した通り、MNIST(手書きの数字0~9がどの数字かを判別する問題)を題材としますので、「教師あり学習」を使ってニューラルネットワークを学習させるということになります。
ニューラルネットワークの学習
前回のブログでニューラルネットワークの構成要素として 重み と バイアス というものがあることを紹介しました。
ニューラルネットワークの学習とは、ネットワークが入力データを受け取ってモデルの作成者が意図したデータを出力するようにニューラルネットワーク内のこの「重み」「バイアス」といったパラメータを調整することを指します。
基本的な学習の流れは以下の通りです。
- パラメータの初期値を決める
初期値は一定のルールで事前に決定するか乱数によって与えられます。 - データをネットワークに通す(入力を与えて出力を得る)
- ニューラルネットワークの出力と正解との誤差を計算する
- 3で計算した誤差が小さくなるようにパラメータを少し変動させる
- 2~4を繰り返す
ニューラルネットワークの学習では一般的にこれを 勾配降下法 や 誤差逆伝搬法 といった道具を用いて行います。勾配降下法はよりよいパラメータに遷移させるための考え方、誤差逆伝搬法はニューラルネットワークの大量のパラメータに対してどう効率よく計算していくかの手法になります。これによって作成者は入力データ上のどこにどんな意味のデータが存在するか、といったことを深く考えることなく、学習によって目的にあった出力を得ることが可能になるというわけです。
一般的なAIのプログラミングでは、この出力データのために重みやバイアスといったパラメータを最適化(オプティマイズ)する機能(オプティマイザ)はライブラリで用意されたものを使いますが、今回はスクラッチ開発をするためこの部分に関しても直接実装することになります。
学習の進め方
勾配降下法
教師あり学習で行うニューラルネットワークの学習は「正解データ」と「ネットワークの出力」の誤差(あるいは損失とも言います)が小さくなるようにパラメータを少しだけ変動させる、ということを繰り返します。
この際、この誤差を計算する式(関数)を 誤差関数(あるいは損失関数、目的関数) と言います。この関数は「入力値」「出力値」「正解データ」「パラメータ」から「誤差」を計算するものです。
誤差関数は正解との誤差を表現できていればなんでも構いません。単純な「誤差」=「正解」-「出力」のようなものでも良いですし「誤差」=(「正解」-「出力」)^2のようなものでも良いです。
さて、例えば1と入力して2が出力されました、その際に実際の正解は3だったとします。パラメータがw1とw2の2つあると考えると、この場合の正解との誤差はこの2つのパラメータの値がどうかによって変動することになります。w1とw2の値によって誤差が決まる、というわけです。それはグラフにするとこんなイメージになります。
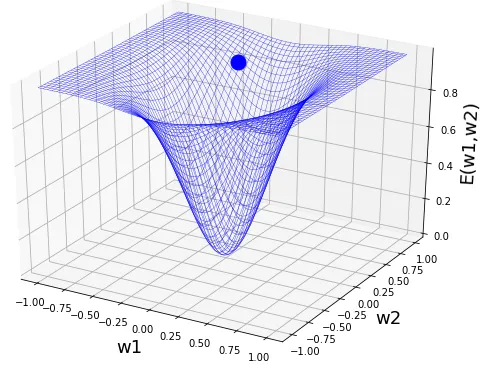
青い点が現在のパラメータと考えてください。縦と横がパラメータ、高さは誤差の大きさです。パラメータによって誤差の値が大きくなったり、小さくなったりすることが視覚的に分かるかと思います。上記の図は1つのくぼみがあるようなグラフになっていますが、この形は誤差関数の形や入力値、出力値によって様々になります(くぼみや山がたくさんある場合もあります)。
学習というのは正解に近づける、すなわち誤差(=損失)を小さくすることが目的ですから、このグラフ上でもっとも低い位置を示すパラメータを探索する、ということが学習なわけです。
つまり前述の学習の手順は、今のパラメータである青い点の位置をどこに移動させれば今より良くなるかを考え、更新、これらを繰り返すということになります。
それをどのように行うかというと、例えば青い点の位置の「傾きの方向」や「傾きがどのくらい急か」を考えるとどっちの方向に動かせばより低い位置に移動できるかが分かるような気がしませんでしょうか。例えば青い点がボールで、そのボールが坂を転がるようなイメージです。
このように誤差関数を坂、つまり 勾配 に見立てて、誤差のより低い位置を示すパラメータを探索するために、この勾配を降下していくようにパラメータを更新していく方法を 勾配降下法 といいます。
それでは具体的にどうやって計算するのかですが、これには 微分 を使います。
微分して求めた導関数から接線の傾きがわかることは覚えていますでしょうか。これを使って今のパラメータでの勾配上の傾きを計算します。ただし、一般的な微分は単一パラメータに対しての操作ですが、前述の例であればパラメータがw1、w2の2つです。このような場合は 偏微分 を行います。
通常の微分の考え方は1つのパラメータが少しだけ遷移したときに結果はどのくらい影響を受けるのかを考えることです。偏微分での考え方は1つのパラメータに注目したときに他のパラメータは固定されている(つまり定数)と考えます。そのうえで注目したパラメータが少しだけ遷移したときに結果がどのくらい影響をうけるのかを考えます。複数のパラメータの場合はこれをパラメータの数だけ実施します。
前述のグラフで考えてみましょう。
まずパラメータw1を考える場合、w2は定数と考え、現在のパラメータのw2の値で固定します。イメージは以下のようなものになります。
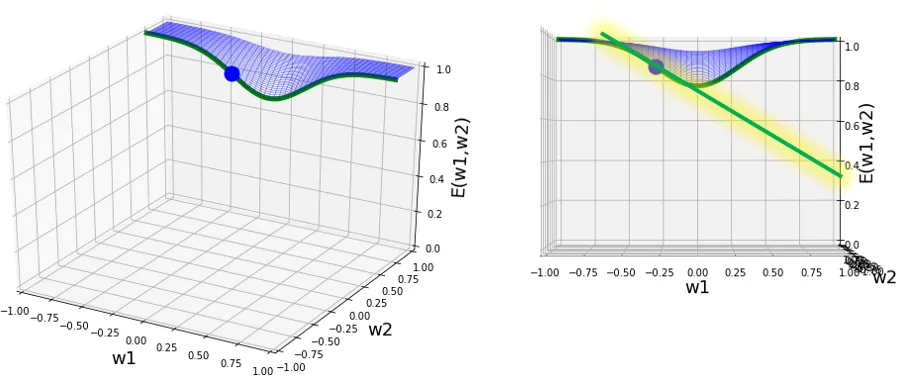
次に同様にw2について考えるとこのようになります。
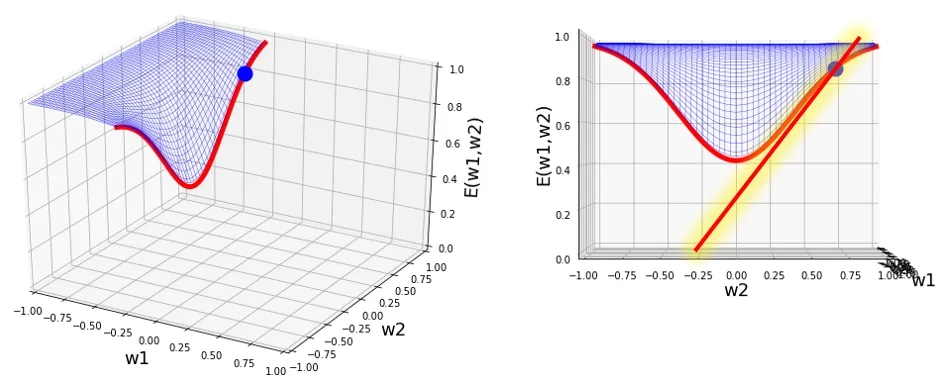
このようにして全てのパラメータでどちらに動かせばよいか分かれば最終的に青い点をどちらに動かせばよいか、その方向がわかります。
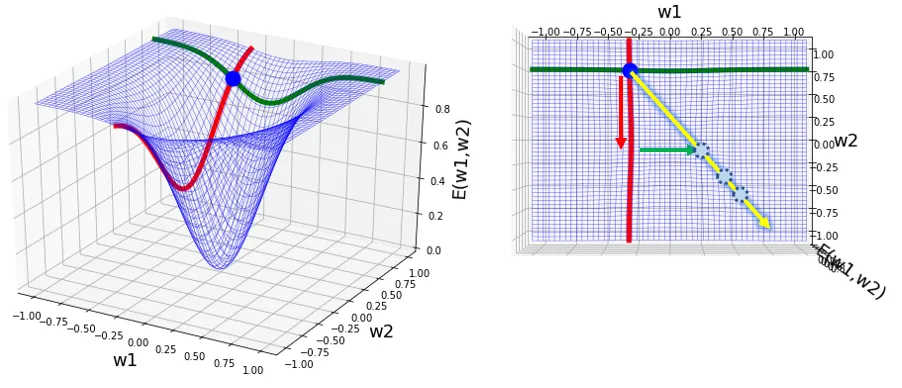 今回は直感的に分かるようにパラメータ2つのケースで3次元のグラフで説明しました。この考え方は以降パラメータが増えていっても変わりません。
パラメータが3つ以上になると今回のように可視化して直感的に理解するのは難しくなりますが、パラメータの数だけ偏微分し、各パラメータの傾きからパラメータの更新する方向を得るという考え方は同じになります。
今回は直感的に分かるようにパラメータ2つのケースで3次元のグラフで説明しました。この考え方は以降パラメータが増えていっても変わりません。
パラメータが3つ以上になると今回のように可視化して直感的に理解するのは難しくなりますが、パラメータの数だけ偏微分し、各パラメータの傾きからパラメータの更新する方向を得るという考え方は同じになります。
これでパラメータを更新する方向は分かりました。それではその方向にどのくらい移動させてやれば良いのでしょうか?これは一般的に学習率という変数でコントロールします。
前述の手順でパラメータを 少し変動させる と表現しました。パラメータの変動具合は大きすぎればもっとも低くなる誤差の位置を通り過ぎてしまう可能性があり、小さすぎればもっとも低くなる誤差の位置に移動するまでに時間が掛かりすぎてしまいます。これをいい塩梅にコントロールするのが 学習率 という存在です。
この学習率は定数にすることもあればパラメータを更新するたびに変動させたりすることもあります。
以上のことからパラメータの更新式は以下のように表すことが出来ます。
![]()
wはパラメータ、E( )は誤差関数を表し、αは学習率、∇(ナブラ)は微分を表しています。wの添え字tは時系列を示し、t+1で次のパラメータを表現しています。
つまりこれを日本語で表現すると
「前回のパラメータ」から「誤差をパラメータで微分して学習率を掛けたもの」を引いて次のパラメータに更新するよ、という意味になります。
誤差逆伝搬法
パラメータを更新していく方法として用いられるのが誤差逆伝搬法です。具体的にニューラルネットワークのパラメータを前述の更新式を使ってどう更新していくのか見ていきましょう。
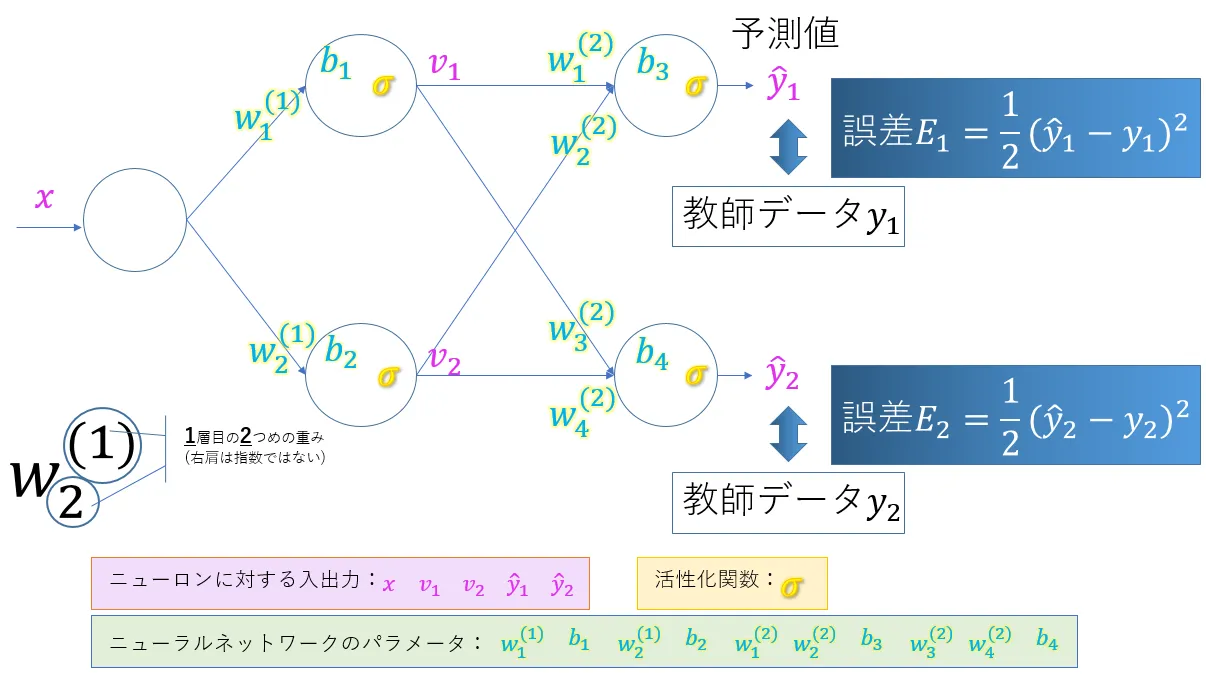
隠れ層にノードが2つの単純なニューラルネットワークです。
今回誤差Eとして、![]() を導入しています。誤差を2乗して2で割っています。2乗しているのは差がマイナスになっても大きさを大小で表現するため、2で割っているのは微分したときに式の表現を簡単にするためです。勝手にそんなことをしてもいいの?と思われる方もいらっしゃるかもしれませんが、学習(パラメータの更新)の目的は出力と教師データの誤差をなくすことです。つまり重み
を導入しています。誤差を2乗して2で割っています。2乗しているのは差がマイナスになっても大きさを大小で表現するため、2で割っているのは微分したときに式の表現を簡単にするためです。勝手にそんなことをしてもいいの?と思われる方もいらっしゃるかもしれませんが、学習(パラメータの更新)の目的は出力と教師データの誤差をなくすことです。つまり重みwやバイアスbの変化によるEの 変化量が大事(パラメータを更新して前回の誤差より相対的に小さくなっていることが大事)であり誤差そのものの絶対的な数値の大小は重要ではないため、問題ありません。
活性化関数としてはシグモイド関数(σ)を用いています。
※シグモイド関数
シグモイド関数は以下のようなものです。
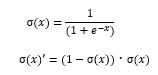
上側の式がシグモイド関数、下側はシグモイド関数の微分の式になります。微分すると自身の掛け算の形で簡単に表現できるのがシグモイド関数の特徴の1つです。
まずこのネットワークの第二層の1つめの重みを更新することを考えてみましょう。
出力層にもっとも近い層のパラメータの更新
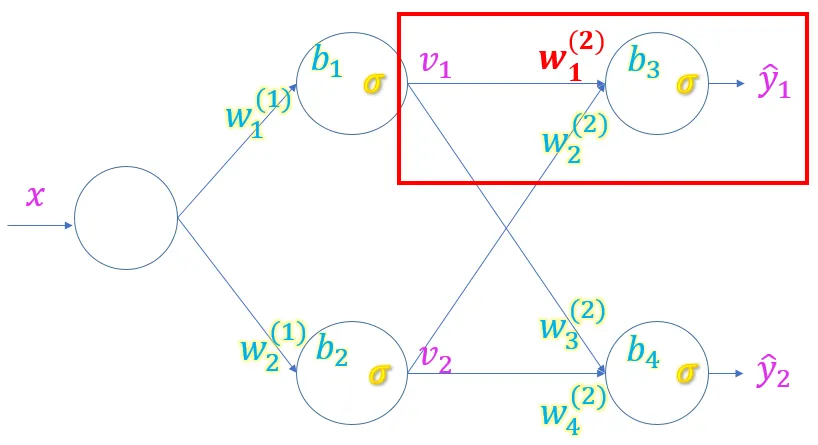
図の赤字(2層め、1つめの重み)パラメータの更新を考えます。
勾配降下法におけるパラメータの更新式は次のようなものでした。
![]()
2項めの偏微分さえ計算できればあとは学習率を掛け算して引くだけですね。それでは今回の場合のこの偏微分の部分を考えてみましょう。
赤枠の中では次のようなことが起こっています。
- 2つのニューロンに対する入力に対してそれぞれ重みを掛け、それらとバイアスを合計する。
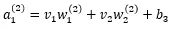
- 1.で計算した結果を活性化関数に通してニューロンの出力(予測値)を得る。
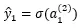
- 2で計算した予測値と正解データから誤差関数を使って誤差を計算する
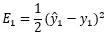
これを踏まえて、誤差関数(E)を更新したいパラメータ![]() で偏微分するということを考えます(数学的に記述すると
で偏微分するということを考えます(数学的に記述すると![]() となります)。
となります)。
偏微分を 微分の連鎖律(※) を用いて記載すると以下のように書けます。
※連鎖律
複数の関数が合成された 合成関数 を微分するとき、その導関数がそれぞれの導関数の積で与えられるという関係式のことを 連鎖律 といいます。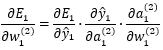
つまり、前述の1,2,3の式をそれぞれ偏微分したものを掛けると求められるということです。よって、求めたい偏微分は以下の式であるということが分かります。
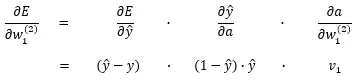
これをもともとの更新式に合わせるとパラメータの更新は以下の式で行えることになります(←は更新を表しています)。
![]()
上記が出力層にもっとも近い重みの更新式になります。バイアスについては1の式をバイアスで偏微分することになり、v1ではなく1が残る、という違いのみになりますので、以下のようになります。
![]()
これがもっとも出力層に近いニューロンのパラメータの更新式になります。
中間層のパラメータの更新
中間層(出力層にもっとも近い層以外)のパラメータの更新です。
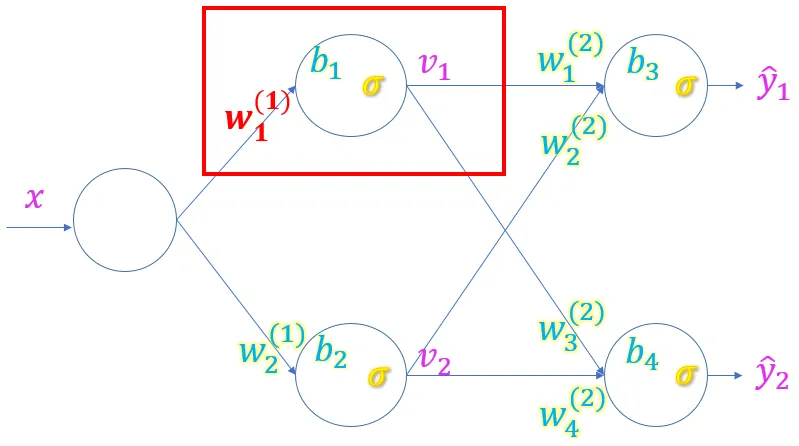
図の赤字(1層めの1つめの重み)パラメータの更新を考えます。
パラメータを更新するためには誤差関数を微分する必要がありますが、今回のパラメータを計算した結果は2つの出力に利用されています。複数の出力に影響を与えている場合はその結果のすべての誤差を考慮する必要があります。
今回のパラメータの更新に関わる式を整理してみましょう。
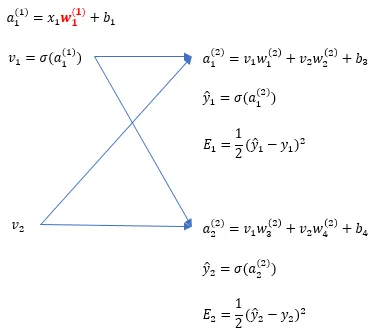
各ニューロンの内部で行っている計算は同等の内容で、入力値にそれぞれ重みを掛け算し、それを入力分繰り返し、バイアスを加えて活性化関数に渡して出力を得ます。
ネットワークの出力はそれぞれの正解データを使って誤差関数で誤差を求めています。
パラメータを更新するのに必要なのは誤差関数を更新したいパラメータで偏微分することですので、今回求めたいものは以下のようになります。
![]()
2つの誤差を足したものですね。そして、これをやはり 連鎖律 を使って表現すると以下のようになります。
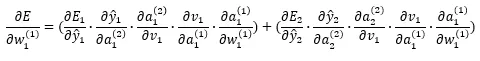
これらを見ると先ほど整理した式を1つずつ偏微分し、出力層側から遡りながら掛け算しているのが分かると思います。
それでは先ほどの連鎖律で表現した式を偏微分して変形してやりましょう。
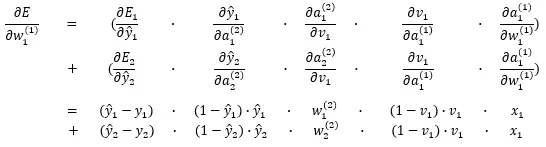
これで更新したい重みパラメータで誤差関数を微分することが出来ました。バイアスの場合は微分した際の結果が1になる部分が変わるだけですので、上記の式の最後が1になるだけ、つまり以下のようになります。
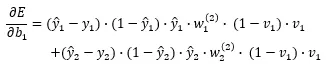
中間層のパラメータの更新はこのようにして行います。層が増えたり、層内のニューロンが増えてもこの偏微分の数が増えるだけでやることは変わりません。やりたいことは「更新したいパラメータで誤差関数を偏微分する」ということですので、あとは必要な分だけ式を合成してやって連鎖律を使って偏微分してやるだけです。
ニューラルネットワークの入力層から出力層に向かってデータが流れていくのを 順伝搬 と言いますが、パラメータを更新する際はこのように計算した誤差が出力層側から入力層側に順伝搬とは逆向きに伝わってくるようになります。そのためこの手法を 誤差逆伝搬法 といいます。
実装
第一回、そして第二回のこれまでの内容でやっとニューラルネットワークを実装する材料が整いました。それでは実際にソースコードを見ていきましょう。
スペースの都合上import文等は割愛しておりますのでご了承ください(使用しているモジュールは全てPython 3.8.3で標準で備わっているものになります)。
class Perceptron: def __init__(self, in_num): self.b = 0.0 # 平均0、標準偏差1の正規分布からランダム self.w_list = [random.normalvariate(0.0, 1.0) for w in range(in_num)]
def __call__(self, data_list, train_flg=True): return self.forward(data_list, train_flg)
# 順伝搬 def forward(self, data_list, train_flg=True): calc_res = 0.0
# 入力値に重みを掛け、それらとバイアスとの総和を計算 for d, w in zip(data_list, self.w_list): calc_res += d * w before_act = calc_res + self.b after_act = sigmoid(before_act)
# 学習時は入力値と計算結果を保持 if train_flg: self.in_data = data_list self.before_act = before_act self.after_act = after_act
return after_actまずはパーセプトロンの実装です。前の層から接続されたニューロンの数だけ重みパラメータと1つのバイアスパラメータを持ちます。やることは入力値とそれぞれに対応した重みを掛け算し、それにバイアスを加えて活性化関数(今回はシグモイド関数です。ソースコードは別途後述)に通して出力値を得ることです。
順伝搬は学習時以外に予測時にも行われることになりますが、学習時は逆伝搬でパラメータの更新を行う場合に備えて計算に必要な値を保持しています。
class Layer(): def __init__(self, in_num, out_num) -> None: self.in_num = in_num self.out_num = out_num self.node_list = [Perceptron(in_num) for n in range(out_num)]
def __call__(self, in_data, train_flg=True): return self.forward(in_data, train_flg)
# 順伝搬 def forward(self, in_data, train_flg = True): res_list = [] for n in self.node_list: res_list.append(n(in_data, train_flg))
return res_list次は層クラスです。層は「前の層からの入力の数」、「次の層に対する出力の数」の情報で定義されます。「層に対する入力の数」は「層内のニューロンに対する入力」の数に等しく、そのまま「ニューロンが内部で保持する重みパラメータの数」でもあります。また、層の出力の数は層内に保持するニューロンの数と等しいです。
順伝搬では入力値として受け取ったデータリストを各ニューロンに渡し、各ニューロンが算出した出力値を出力値用のリストにして返却しています。
class Optimizer: def __init__(self, layers, lr=0.1): self.lr = lr # 学習率 self.layers = layers # ネットワークの層 self.calc_results = {}
def back_prop(self, t_data_list): # 各層の処理 for l_idx, layer in enumerate(self.layers): # 各ノードの処理 for target_node_index in range(len(layer.node_list)): node = layer.node_list[target_node_index] # 重みの更新 for w_indx, w in enumerate(node.w_list): node.w_list[w_indx] = w - (self.lr * self.d_calc(l_idx, target_node_index, t_data_list) * node.in_data[w_indx]) # バイアスの更新 node.b = node.b - self.lr * self.d_calc(l_idx, target_node_index, t_data_list) self.calc_results.clear()
def d_calc(self, l_idx, j, t_data_list): # 計算済みの結果があればそれを使う result_key = (l_idx, j) if result_key in self.calc_results: return self.calc_results[result_key]
# 最終層の場合 if l_idx == len(self.layers) -1: result = (self.layers[l_idx].node_list[j].after_act - t_data_list[j]) * sigmoid_d(self.layers[l_idx].node_list[j].before_act) self.calc_results[result_key] = result else: result = 0.0 for i, node in enumerate(self.layers[l_idx+1].node_list): result += self.d_calc(l_idx+1, i, t_data_list) * node.w_list[j] * sigmoid_d(self.layers[l_idx].node_list[j].before_act) self.calc_results[result_key] = result
return result次はオプティマイザクラスです。オプティマイザは最適化、つまりニューラルネットワークの学習の肝であるパラメータの更新を行います。今回解説を行った 誤差逆伝搬法 を実際に実装している箇所になります。
back_prop()では指定されたニューラルネットワーク(コード上の層リスト=layers)の各層、各ニューロンの重み・バイアスパラメータを1つ1つ入力層側から順番に更新していきます。
d_calcでは更新式の微分の部分にフォーカスした計算処理を行う部分です。層が増えるたびに再帰呼び出しにより計算が繰り返され、出力層側から計算されていくことになります。
今回解説したように誤差逆伝搬法を使うと出力層側から入力層側に計算結果が伝搬していきます(d_calcで再帰的に実施している箇所)。そのため、最初の層のパラメータの更新を行うと、その時点で次の層以降の計算も必然的に行われることになります。パラメータの更新を1つ1つ実施していく過程で全て愚直に計算すると何度も同じ計算を行うことになるため、そうならないように1度計算した結果は保持していくようにしてあります。
パーセプトロンとオプティマイザで使用しているシグモイド関数とシグモイド関数の微分は以下の通りです。
# シグモイド関数def sigmoid(num): return 1 / (1 + math.exp(-num))
# シグモイド関数の微分def sigmoid_d(num): return (1 - sigmoid(num)) * sigmoid(num)ここまでのクラス、関数を用いてニューラルネットワークモデルクラスを実装します。
class NN: def __init__(self): self.layers = []
def add_layer(self, layer): self.layers.append(layer) return self
def train(self, data_list, t_data_list, test_data_list, test_t_data_list, epoch=10, debug_flg=False): opt = Optimizer(self.layers, lr=0.25) for i in range(epoch): # データ分ループ i_cnt = 0 for data, t_data in zip(data_list ,t_data_list): # 順伝搬 nn_output = self.forward(data, True)
# 学習50回ごとにMSEをログ出力 if debug_flg & (i_cnt%50 == 0): tmp_calc_error = 0 # MSE(平均二乗誤差を算出) for r, t in zip(nn_output, t_data): tmp_calc_error += (r - t)**2 calc_error = tmp_calc_error / len(nn_output) logger.debug('epoch:' + str(i) + ', ite:' + str(i_cnt) +', error:' + str(calc_error))
# 逆伝搬 opt.back_prop(t_data)
i_cnt += 1
# 確認用のデータを使って精度を確認 accuracy = self.calc_acc(test_data_list, test_t_data_list) logger.debug('acc = ' + str(accuracy))
logger.info("train finished")
def calc_acc(self, test_data_list, test_t_data_list): ok_count = 0 for test_data, test_t_data in zip(test_data_list, test_t_data_list): # 順伝搬 nn_output = self.forward(test_data, False)
# ネットワークが予測した数値(最大index)を取得 max_value = max(nn_output) nn_max_index = nn_output.index(max_value)
test_max_index = test_t_data.index(1)
if nn_max_index == test_max_index: ok_count += 1
return ok_count / len(test_data_list)
def forward(self, in_data, train_flg): # 順伝搬 before_layer_out = None for l in self.layers: if before_layer_out == None: before_layer_out = l(in_data, train_flg) else: before_layer_out = l(before_layer_out, train_flg) return before_layer_out
def predict(self, data): output = self.forward(data, False) max_value = max(output) return output.index(max_value)具備しているメソッドは以下の通りです。
| メソッド名 | 概要 |
|---|---|
| add_layer | 層を追加するメソッドです。 |
| train | 学習メソッドです。学習用の入力データとラベルデータ、精度確認用の入力データとラベルデータを受け取って学習を行います。学習しながら誤差をログ出力しており、出力結果から学習が進んでいるかを確認できます。 |
| calc_acc | 精度計算メソッドです。確認用データを用いてコールされた時点のネットワークの精度を計算します。精度は(正解数/予測数)で求めています。 |
| forward | 順伝搬メソッドです。入力層から順番にデータを通して出力を得ます |
| predict | 予測メソッドです。現在のネットワークにデータを渡して予測結果を得ます。28x28の画像データをフラットにした784個の数値データを入力に、0~9のどの数字かを返却します。 |
それでは最後に上記のモデルを使ってMNISTを使った手書き数字の分類モデルを学習させる処理を実装してみましょう。
def train_main(): model = NN()
x_data, y_data = get_mnist_data()
model.add_layer(Layer(784,20)) model.add_layer(Layer(20,20)) model.add_layer(Layer(20,10))
model.train(x_data[0:5000], y_data[0:5000], x_data[5000:5100], y_data[5000:5100], epoch=20)
return model
if __name__ == '__main__': model = train_main()get_mnist_data()はスペースの都合上割愛しますが、ダウンロードしたMNISTのデータを読み込み入力データと対応する正解データを取得できるようにしています。それぞれのデータは以下のようなものになります。
x_data
ニューラルネットワークの入力用のデータ。縦28x横28の画像データをフラットな数値配列にしたもの(数値はMin-Max法により正規化しています、詳細は割愛)。1データが784個の数値のリスト、それを60000データ分保持したPythonリスト。y_data
正解データ。1つの正解データは0~9までのどの数値を表すかを0,1で表現したもの。1データが10個の数値リスト、それを60000件分保持したPythonリスト。1つのデータは例えば正解が0なら[1,0,0,0,0,0,0,0,0,0]、正解が3なら[0,0,0,1,0,0,0,0,0,0]といった形
このようなデータで、x_dataとy_dataはリストの順番で対応付けされるデータです。
ニューラルネットワークは入力が784、20個のニューロンを持つ中間層が2層、そして出力層という構造で定義しています。
学習には取得したデータの内の5000データ、確認用のデータには100データ使用し、20エポック(エポックというのは学習の単位です。指定した学習データを全て投入して1エポック、と表現します)の学習を行うように指示しています。
さいごに
ずいぶん長くなってしまいましたので、今回のブログではここまでにしたいと思います。
次回のブログで今回スクラッチしたニューラルネットワークを動作させるとどうなるかについて書きたいと思います。

