
[!] この記事は公開されてから1年以上経過しています。情報が古い可能性がありますので、ご注意ください。
はじめに
これまで2回に渡って「ニューラルネットワークをスクラッチする」と題してブログを書いてきました(第一回・第二回)がそれも今回で最後となります。
今回の記事では「前回提示したソースコードを用いて実際にMNISTの学習を行った結果がどうであったのか」について記載するとともに、今回実施した「学習をうまく進めるためのポイント」について記載したいと思います。
動作確認の前に
今回のニューラルネットワークの学習ではMNISTのデータの先頭から5,000番目までのデータを学習に、そこから100個のデータを精度の確認に使用しています。それぞれのデータの内訳は以下の通りです。
■学習データ
| 数字 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 個数 | 479 | 563 | 488 | 493 | 535 | 434 | 501 | 550 | 462 | 495 |
■確認用データ
| 数字 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 個数 | 12 | 11 | 6 | 11 | 11 | 8 | 12 | 10 | 11 | 8 |
今回のニューラルネットワークは手書き数字のデータを1つ入力すると10個の数値を出力します。この出力は10個の数値の中で正解の位置が1、それ以外が0になるような数値で、以下のようなイメージです。
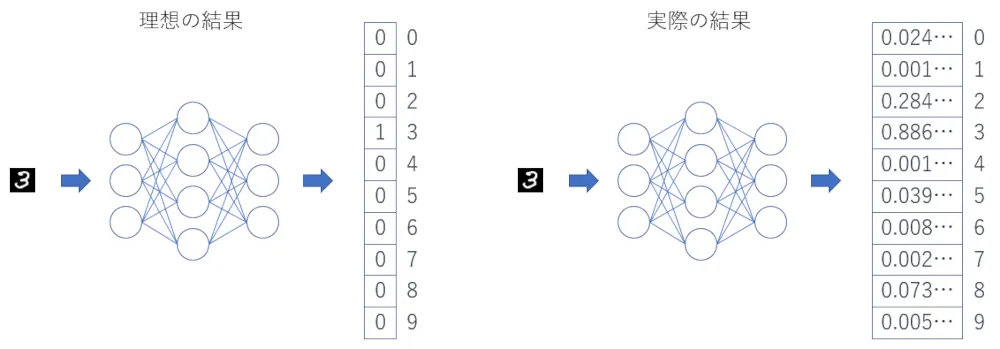
ニューラルネットワークの出力としての理想は上記左図のような1,0の数値なのですが、実際に学習したモデルがあらゆる入力に対して0か1のみの出力を行う(正解との誤差を0にする)ことは困難(というか不可能)です。また、多くのAIで解決したいタスクは、既存のデータを使って学習し、それを踏まえて学習には使用していない未知のデータを使って予測することです。そのため、モデルの予測結果はある程度のあそびのような誤差をあえて残している状態が望ましい、ということになります。そのような誤差が残った結果を、タスクをうまく達成可能にするバランスで利用するのがAIを使ったソフトウェアということです。
今回ニューラルネットワークの予測結果としては上記右図のような10個の数値の中で最も大きい数値を出力した位置を採用することにしています。
もしかしたらこのようにニューラルネットワークの出力を都合よく解釈することに納得いかない方もいらっしゃるかもしれません。しかし本来の目的、すなわち今回であれば「手書きの数字が0~9のどれにあたるのか」という問題ですが、この目的を達成することが重要であり、「ぎりぎり1だった」とか「確実に4だった」などのような確信度について今回は求めていないため問題ありません。
解釈の幅について
このような解釈の幅はAIを使って解決したいタスクによって変わります。例えば人の命に関わる病気の診断等であれば、より厳密な判断が必要となってくるでしょう。逆に入力に対してそれなりに精度は欲しいがいつも同じ値ではない方がよい(例えばゲームのキャラクターの行動など)場合は有力な候補の上位いくつかからランダムに選択するような解釈を行う場合も有効となります。動作確認
それでは学習を実行した結果を見てみましょう。
2022-02-10 17:03:28,606 DEBUG epoch:0, ite:0, error:0.41308983557133622022-02-10 17:03:29,577 DEBUG epoch:0, ite:50, error:0.087588846442598322022-02-10 17:03:30,569 DEBUG epoch:0, ite:100, error:0.11560362722952525・・・中略・・・2022-02-10 17:38:26,505 DEBUG epoch:19, ite:4950, error:1.6179463481047882e-052022-02-10 17:38:27,827 DEBUG acc = 0.92022-02-10 17:38:27,827 INFO train finished上記は実行した際のログの一部を記載しています。
出力されたログから開始直後は0.4130898355713362だった誤差が1.6179463481047882e-05つまり0.000016179463481047882まで小さくなっていることが分かります。
また、学習したモデルの精度は0.9、つまり精度確認用のデータを判定させた際に100個のデータ中90個のデータを正しく判定できたということになります。
モデルの予測結果から見てみると、スクラッチしたニューラルネットワークでもなかなかの精度で判定できるモデルが学習できたと言えそうです。
今回パラメータの初期値を標準正規分布からランダムに取得した数値を用いるように実装しましたので、実行するたびに学習の進み方や最終的な精度は少しブレることがありますが概ね9割前後の精度に落ち着くかと思います。
それではログの情報から学習が進むごとに誤差と精度がどう変化していっているのかを見てみましょう。
学習状況を可視化
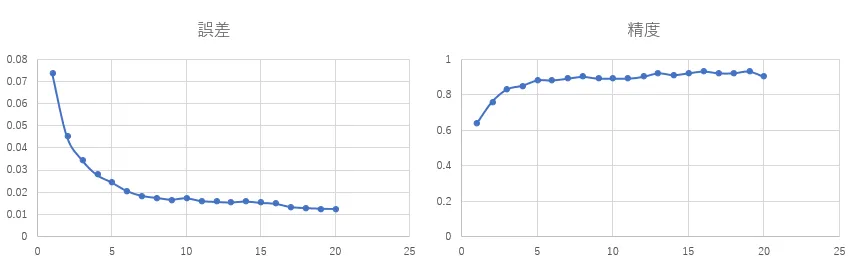
学習は20エポック実施しており、誤差は1エポックごとの平均値、精度は1エポック学習が終了したごとに出しています。
今回のニューラルネットワークの学習は1データ通すごとにパラメータを更新するオンライン学習という手法を取っているため、1エポックでは5,000回のパラメータの更新が行われていることになります。
最初の精度が既に60%以上となっているのは5,000回の更新が行われた結果が最初の精度だからです。
誤差、精度ともに20エポックの学習で概ね限界まで学習している(誤差の降下がとまっている)ように見えるのでこれ以上学習しても精度はあがらなそうに見えます。
モデルの結果の観察
次に学習したモデルが実際にどんな文字を間違えているのか、その文字でどのような出力を行っているのか見てみましょう。

上記は精度の確認に使用した100文字を画像化したものです。左図は文字をそのまま、右図は誤って判定した文字を赤枠で囲ったものになります。今回実施した結果は100文字中90文字に正解していましたので右図でその対象の10文字が指し示されています。
上記左図を見ると、中には人間が見ても非常に判断に困るような文字が含まれていることがわかりますね。このようにMNISTのデータは人間が判定を行った場合でも精度100%で判定するのは困難なものになっています。
それでは今回スクラッチしたニューラルネットワークはこれらをどのように判断したのでしょうか。
以下に判定を誤った10文字について、モデルが出力した結果と正解を一覧で示します。
| 文字 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 予測 | 正解 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ① | 0.00 | 0.00 | 0.00 | 0.00 | 0.04 | 0.00 | 0.00 | 0.00 | 0.00 | 0.99 | 9 | 4 | |
| ② | 0.00 | 0.00 | 0.00 | 0.09 | 0.00 | 0.03 | 0.00 | 0.00 | 0.00 | 0.02 | 3 | 2 | |
| ③ | 0.00 | 0.00 | 0.04 | 0.00 | 0.00 | 0.37 | 0.00 | 0.00 | 0.00 | 0.02 | 5 | 9 | |
| ④ | 0.00 | 0.00 | 0.00 | 0.00 | 0.34 | 0.00 | 0.00 | 0.00 | 0.00 | 0.88 | 9 | 4 | |
| ⑤ | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.68 | 0.00 | 0.00 | 0.22 | 0.00 | 5 | 8 | |
| ⑥ | 0.09 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.04 | 0.00 | 0.09 | 9 | 0 | |
| ⑦ | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.41 | 0.05 | 8 | 9 | |
| ⑧ | 0.06 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.29 | 0.00 | 0.29 | 0.00 | 6 | 0 | |
| ⑨ | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.11 | 0.00 | 0.98 | 9 | 7 | |
| ⑩ | 0.00 | 0.00 | 0.00 | 0.00 | 0.53 | 0.00 | 0.00 | 0.00 | 0.00 | 0.59 | 9 | 4 |
表内0~9に対応する数値はブログの表示領域の都合上小数点第3位を四捨五入して表示しています。赤字は0~9の中でモデルが最も高く示した数値(モデルの予測としている数値)、青字はその次に高く示した数値です(同じ数値になっているものもありますが丸め込みでそうなっているだけで値は赤字のものが高かったものになります)。
この差が大きいものはモデルが確信を持って判定しており、逆に差が小さければ判断に迷っているように解釈することができますね。さらに青字が正解であれば正解との間で迷った結果誤っている、青字も正解ではないのであればモデルは今回の学習で対象の文字を学習することが困難だったと言えそうです。
手書きの数字と結果を見くらべてみると、①の結果などは人がみても9と言われれば9に見えますし、4だと言われればまぁそうなのかと納得できるレベルなのかという気はします。一方で⑤は個人的には6に見える気がしますが正解は8でモデルの判定は5となっています。
人間が手書きの数字を判断するとき、意識せずとも自分の知識と経験から判断していますが、これは当然これまで過ごしてきた文化、触れてきた数字によって大きく異なってきます。モデルもそれと同様に、このような判断をするのは学習したデータの影響によるものということになります。
今回の結果を見ると4を9と誤るケースが多いようです。このような場合学習データに4と9のデータを増やしてやる等の対策が考えられそうです。
さて、今回はこのような結果となりました。今回のモデルは前述の通り処理中にランダム性を含んでいるため、この結果はあくまで一例であり、実行するたびに変わることをご了承いただければと思います。実際に筆者が何度か実行した際に同じ文字を精度確認に使った場合でも成功率は前後しましたし、判定を誤る文字も変化しました(毎回誤る文字もあれば実行するたびに成功したり失敗したりした文字もありました)。
今回は実行にあまり時間が掛からないようにMNISTが学習用として用意しているデータ60,000件のうち5,000件のデータを学習してみました。スクラッチしたモデルで学習データの規模も縮小して実施した結果の精度90%前後というのはそれなりの結果と言えそうですよね。
ところでそれなりの精度に学習できた今回のモデルなのですが、ニューラルネットワークの仕組みをただ実装すればそれだけで簡単に得られるものなのかというと実はそうではありません。前回ソースコードを紹介した中でも簡単にしか触れなかった部分にニューラルネットワークの学習をうまく進めるコツのようなものが含まれています。
学習をうまく進めるコツ
今回学習を進めるために導入した以下の2つのアプローチについて紹介したいと思います。
- 入力データの正規化
- 重みパラメータの初期値の設定
入力データの正規化
正規化の方法にもいくつかありますが、今回はMin-Max法と呼ばれる手法で入力データを正規化しています。この手法によって正規化を行うと、分散したデータ群をそのデータ同士の相対的な距離感を保ちながら0~1の範囲に変換することができます。
今回ニューラルネットワークに入力するMNISTのデータは白黒の手書きの数字画像のデータで、以下のようなものです。
- 1つの画像が縦28×横28のデータ784個の数値データ
- 1つの数値は0(黒)~255(白)
つまりニューラルネットワークには0~255の数値が1回で784個投入されるということです。Min-Max法を使ってこれを0~1の間の数値784個に変換しています。
例えば正規化しないと学習はどうなるのでしょうか。実際にやってみた結果をみてみましょう。
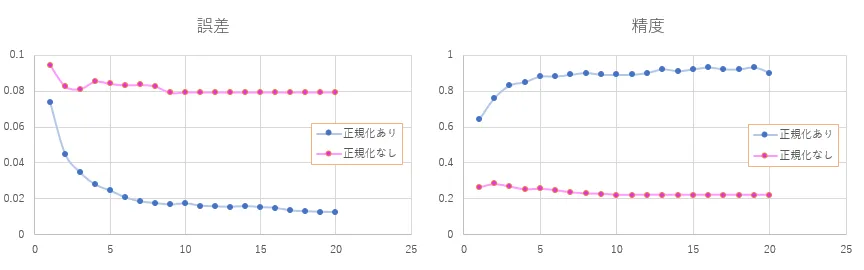
青いラインが正規化ありのグラフ(前述の学習状況を可視化した際のグラフと同じデータ)、紫のラインが正規化なしのグラフです。正規化なしだと学習を繰り返しても誤差がなかなか下がっていかず9エポック以降はほとんど動きがありません。精度で見ても学習を進めても上がっていく傾向がみられません。どうしてこんなことが起こるのでしょうか。
ニューラルネットワークはスクラッチして全て自分で実装しているのでソースコードのどこかをみればこのカラクリがわかるはずです。
def forward(self, data_list, train_flg=True): calc_res = 0.0
# 入力値に重みを掛け、それらとバイアスとの総和を計算 for d, w in zip(data_list, self.w_list): calc_res += d * w before_act = calc_res + self.b after_act = sigmoid(before_act)
# ・・・中略・・・
return after_act上記はニューロン(パーセプトロンクラス)の順伝搬のソースの抜粋になります。data_listに入力値のリストが入ってきます。見ての通り受け取った入力値1つ1つに、それぞれに対応する重みパラメータwを掛け算し、それらとバイアスbを全て足したものをシグモイド関数に渡して出力値を得ています。シグモイド関数のソースは以下です。
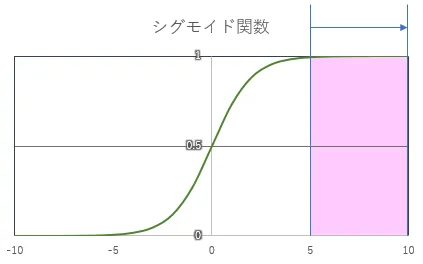
# シグモイド関数def sigmoid(num): return 1 / (1 + math.exp(-num))これだけではよくわからないですね。グラフにしてみるとシグモイド関数とは以下のようなものになります。
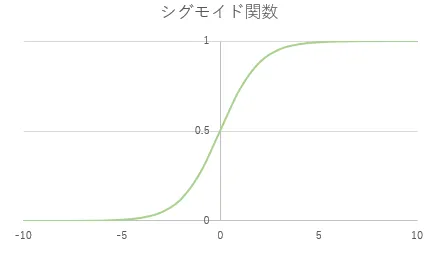
シグモイド関数とはこのように入力として\(-∞ {~} ∞\)をとり、出力は\(0{~}1\)となります。
さて、正規化しない場合入力層のニューロン内では何が起こるでしょうか。
MNISTのデータをそのまま使った場合の値は\(0{~}255\)でした。この値全てに重みパラメータが掛けられ、それを合計してバイアスとともにシグモイド関数に渡されることになります。もちろん重みパラメータの大きさに依存することにはなりますが、掛け算して足し算するわけですから入力値が\(0{~}255\)の場合、シグモイド関数に渡される数値はそれなりの大きさになりそうですよね。シグモイド関数を見てわかる通り、この関数に渡される値が5を超えた辺りからはもうほとんど1に近い値しか出力されません。
ニューラルネットワークの学習、つまりパラメータの更新式は以下のものでした。
$$ w_{t+1} = w_{t} - \alpha \nabla_{w} E(w) $$
このように誤差関数を微分し、パラメータを少しずつ誤差が小さくなるように調整していきます。しかし、シグモイド関数から出力される値がほとんど1に近い値のみになってしまうと、少しパラメータを更新してもシグモイド関数から出力される値はほとんど1に近い値から変動しません。このため、学習を繰り返しても誤差が下がらず、精度も低いままとなってしまいます。
そこで正規化の出番です。入力値を正規化する、つまり\(0{~}255\)の値だったものを\(0{~}1\)にしてやります。こうすることでシグモイド関数のなめらかに適度に値が変動している部分を利用することが可能になり、学習をうまく進めることができるというわけです。
重みパラメータの初期値の設定
重みパラメータの初期値はどのように決めればよいのでしょうか?それには重みパラメータの初期値がどんな意味を持つのかを理解する必要があります。
今回ニューラルネットワークの学習、つまりパラメータの更新には勾配降下法を使って行いました(前回のブログ参照)。勾配降下法では以下のように損失関数を勾配に見立て、その勾配を球(パラメータの位置)が転がるようにパラメータを更新していきます。
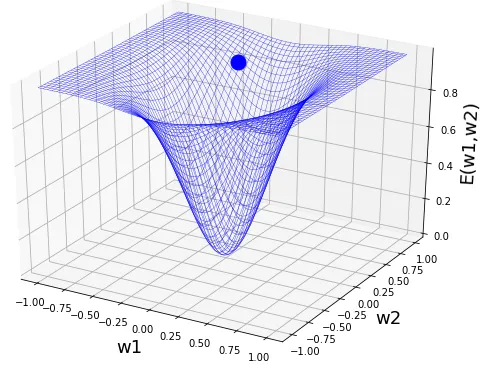
つまり、パラメータの初期値というのはこの勾配を転がり始める最初の場所ということになります。
勾配はタスク(扱うデータ)やネットワークの構造(ユニットの数や層の深さなど)によって様々な形を取る可能性があり、それをどのように転がっていくのかというのはオプティマイザ(前回のブログ参照)によって変化します。学習の目的はこの勾配の最も低い場所に到達することですが、転がり始める場所・勾配の形・転がり方によっては最も低い場所までの間にある少し低い場所にハマってしまったり、別な方向に転がってしまったり、あるいはものすごく時間がかかってしまったりしてしまうのです。このためAIエンジニアは最も良くより低い位置に到達できるようにこの転がり始める場所・勾配の形・転がり方などの組み合わせを(多くはtry and errorによって)探す必要があるのです。
さてそれでは重みパラメータの初期値をどのように決めればいいかということですが、ここまできて何なのですが、ベストな初期値を1発で求めるような手段は基本的に存在しません。想像していただけるとわかると思うのですが、ベストな転がり始めの場所は最も低い場所を探すのと同じくらい困難なことだからです。ではどうするのか、考え方としては前述の通りAIエンジニアはタスクに応じたよりよい状況を探すためにtry and errorを繰り返しますので、この作業をできるだけ安定的に円滑に行えるような手段を取るということになります。
よく使われる方法は以下のようなものです。
- 特定の値で全て初期化する
- 乱数(ランダム)を用いる
- 学習済みのモデルのパラメータを流用する
- etc...
今回のニューラルネットワークでは上記の乱数を用いる方法で特に正規分布から乱数を生成する方法を選択しました。前回のブログで紹介したソースコードの以下の部分ですね。
class Perceptron: def __init__(self, in_num): self.b = 0.0 # 平均0、標準偏差1の正規分布からランダム self.w_list = [random.normalvariate(0.0, 1.0) for w in range(in_num)] # 以下略random.normalvariate()がそれにあたります。実際に「全て同じ値(0.0)での初期化」と「乱数(random.random()関数を使用)」も実行してみましたので今回の実施結果と学習具合(誤差・精度)がどう変わってくるのか見てみましょう。
ちなみに出力している誤差は前回のブログで示した以下のソースの通りMSE(平均二乗誤差)になります。
以下は前回提示したソースNNクラスのtrain()の一部の抜粋です。
# 学習50回ごとにMSEをログ出力 if debug_flg & (i_cnt%50 == 0): tmp_calc_error = 0 # MSE(平均二乗誤差を算出) for r, t in zip(nn_output, t_data): tmp_calc_error += (r - t)**2 calc_error = tmp_calc_error / len(nn_output) logger.debug('epoch:' + str(i) + ', ite:' + str(i_cnt) +', error:' + str(calc_error))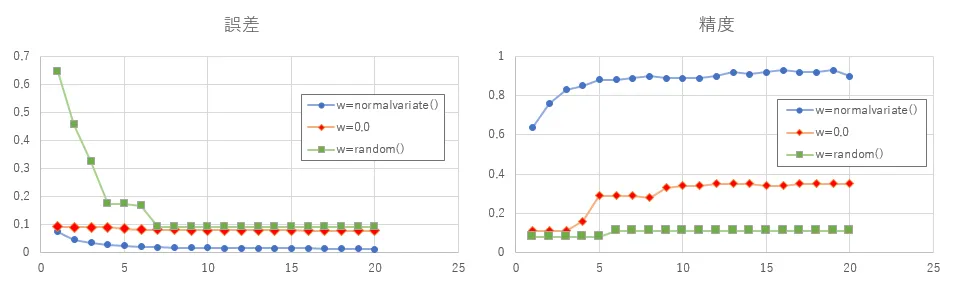
重みパラメータを「全て0.0で初期化した場合」「random.dandom()で初期化した場合」「random.normalvariateで初期化した場合(今回ブログで採用)」の誤差と精度の推移を可視化しました。
全て0.0で初期化した場合、そしてrandom()を利用した場合は一見すると誤差は、小さくなっておりそれなりに正解に近いように見えます。しかし、今回のニューラルネットワークの出力は10個のうち正解の場所を1,他を0で出力するネットワークであり、出力している誤差は平均二乗誤差(正解と予測値を引き算したものを2乗して10で割ったもの)です。つまり全て0を出力するとこの誤差は0.1になります。
よってこの誤差を超えて小さくできるかはひとつポイントになるところになりますが、さきの2パターンに関してはそこをうまく超えられていない印象です。
精度について見てみても0.0で初期化したモデルは多少あがっていますが0.4には至らないくらいで止まっている、random()の方に関しては0.1程度から向上がみられないという形になっています。
精度0.1について考えてみると、今回モデルの予測結果は出力結果の中で最も大きい値を採用していますが、このやり方だと学習がまったく進んでいない状態でも必ず1つの値が選択されることになります。この選択された結果というのが0.1、つまり1/10の正解に対して無作為に選択しても正解できるであろう期待値程度ということになり、全く学習できていないと言えそうです。
詳細は割愛しますが、正規化の場合と同様にスクラッチで実装していることからこのような結果になったのはなぜかをソースコード内の計算の途中や結果などを観察することで調査し、改善案を検討することができます。
結果normalvariate()を使って平均0.0、標準偏差1.0の正規分布から得た値で初期化することで今回の場合は学習がうまく進むことが分かりました。
さいごに
いかがでしたでしょうか。AIという何をやっているのかよくわからないものが、ニューラルネットワークをスクラッチすることにより、中で何が起こっているか少し具体的にイメージできるようになったのではないかと思います。
また、最近ではAIをGUIから簡単に作成し、層の数やユニット数などのハイパーパラメータも自動である程度調整してくれるような機能も提供されていたりしますが、今回のようにスクラッチして中身を理解することで、例えよくない結果になった場合でもそれがなぜなのかを考察し、次の改善アプローチに活かすことができることもご理解いただけたかと思います。
3回にわたって「ニューラルネットワークをスクラッチする」と題して書いてきたブログも今回で終了になります。今回の記事が皆様のよきAIライフに少しでも役立つことができれば幸いです。ありがとうございました。

