量子コンピュータシミュレータを自作してみた

カバー

[！] この記事は公開されてから1年以上経過しています。情報が古い可能性がありますので、ご注意ください。

量子コンピュータシミュレータを自作してみた

はじめに

昨今、量子コンピュータという言葉をよく耳にするようになってきました。

量子コンピュータとは、ざっくり言えば従来のコンピュータよりも特定の分野においてとてつもなく早く結果を導くことができるコンピュータです。

例えば素因数分解は暗号アルゴリズムにも取り入れられるくらい時間がかかる処理で有名です。 素因数分解を利用した 2048 ビットの RSA 暗号を従来のコンピュータで解読しても 1 億年以上かかると言われています。

現在の量子コンピュータでは様々な課題があり 2048 ビットの RSA 暗号を解読することができませんが、課題が解決されれば現実的な時間で解読することができると言われています。

そんな量子コンピュータですが一般の人ではなかなか実機を使うことはできません。クラウドでも提供されていますが、お金がかかるため試しに使ってみるにはハードルが高いです。

しかし最近では量子コンピュータをシミュレートできる Qiskit などのシミュレータライブラリが存在しており、誰でも量子コンピュータが体感できるようになっています。

今回はその量子コンピュータをシミュレートするためのシミュレータ自体を自作してみました。

なぜ自作するのか

最近では Qiskit をはじめとした量子コンピュータシミュレータを使うことで比較的簡単に量子コンピュータをシミュレートすることができます。

しかしライブラリを使うためにはある程度量子コンピュータを知っておく必要はあります。

私自身とりあえず Qiskit を使って量子コンピュータを体感してみようとしたときに「X ゲートとか H ゲートとかって何だ？何をしているんだ？」と疑問が多く、他人のシミュレートした量子コンピュータを参考にしても理解ができず、シミュレートできませんでした。

つまり量子コンピュータのシミュレータライブラリを使用するには、ある程度量子コンピュータについて知っておく必要があります。

そこで今回、量子コンピュータシミュレータを自作しました。 自作することで量子コンピュータを知ることができ、座学だけでは本当に理解していなかったことを体感しながら学ぶことができます。

具体的に何を作るのか

量子コンピュータシミュレータを自作するのですが、まずは量子コンピュータについて簡単に説明します。

量子コンピュータでは「量子ビット」というビットを扱います。詳細は後述しますが、この「量子ビット」は従来のコンピュータにおけるビット(ここでは古典ビットと呼びます)とは違いがあります。

そして、その「量子ビット」に対し量子ゲートと呼ばれる物で量子演算を行って出力を得るのが量子コンピュータです。

量子回路

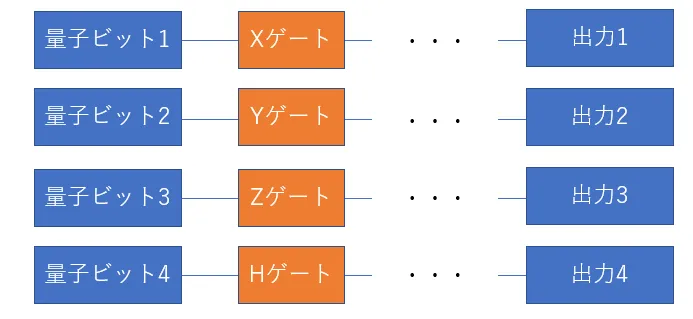
量子コンピュータでは様々な量子ゲートを特定のアルゴリズムに則って組み合わせて最終的に出力を得るということをしています。

今回は任意に量子ゲートを組み合わせることができるシミュレータを自作します。 ただし、目的はあくまで量子コンピュータを理解することなので量子ゲートは基本的なゲートのみを実装します。

つまり、「量子ビット」と基本的な「量子ゲート」を実装し、量子演算できるようにします。どんな回路を組むかはシミュレータを使うユーザ次第となります。

開発要件

実装する機能

・量子ビット/量子ゲートを実装し、量子演算ができる機能

・量子ビットを測定する機能 (測定については後述)

・量子ゲートを任意に組み合わせて回路を作成することができる機能

言語

Python

選択理由：Python ではビルトインで複素数を扱うことができるライブラリが存在しているため。

量子ビットと量子ゲート

作るものは決まりました。

ここまで出てきた「量子ビット」、「量子ゲート」について知らない人のためにプログラムを交えながら説明していきます。

量子ビット

古典ビットは 0 か 1 の状態しかとれないのに対し、量子ビットは 0 と 1 の状態に加え、0 と 1 の「量子力学的重ね合わせ」状態もとることができるビットです。 「量子力学的重ね合わせ」の状態とは、簡単に言ってしまえば 0 にも 1 にもなりうる状態とも言えます。

そして、量子ビットには「測定」という概念があります。 いわゆる「量子力学的重ね合わせ」の状態は前述の通り 0 にも 1 にもなりうる状態ですが、「測定」をすることでその値を 0 か 1 に確定させることができます。逆に言えば、「測定」するまでは 0 でも 1 でもありません。

では「測定」するとどのように値が決まるのか、それを理解するためにもう少し量子ビットについて掘り下げていきます。

量子ビットはブラケット記法という記法で表すことができ、1 量子ビットは以下(1)式で表現できます。

$$ \ket{\psi} = \alpha\ket{0} + \beta\ket{1}・・・(1) $$ ※ \(\psi\)はプサイと読む

ここで \( \alpha,\beta \) は \(|\alpha|^2 + |\beta|^2 = 1\) の関係を満たす複素数です。

ブラケット記法で表現された量子ビットは、「\(|\alpha|^2\)の確率で 0 になり、\(|\beta|^2\)の確率で 1 になる状態」と解釈できます。

例えば、 量子ビット \( \displaystyle \ket{\psi} = \frac{1}{\sqrt{2}}\ket{0} + \frac{1}{\sqrt{2}}\ket{1} \) を「測定」すると、\( \displaystyle |\frac{1}{\sqrt{2}}|^2 = \frac{1}{2} \) なのでそれぞれ\( \displaystyle \frac{1}{2} \)の確率で 0 になったり 1 になったりします。

このように、古典ビットは 0 と 1 どちらかの状態しかとれないことに対して、量子ビットは 0 にも 1 にもなりうる状態(量子力学的重ね合わせ状態)を取れるビットです。

ここまでの量子ビットの概念を古典ビットと比較しながらプログラムで表現してみます。

まずは、古典ビットと量子ビットをプログラムでクラスとして定義すると以下の様なデータ構造になります。

class ClassicalBit: # 古典ビット
  def __init__(self):
    self.value = 0 # value には 0 か 1 が入る


class QuantumBit: # 量子ビット
  def __init__(self):
    self.state = { 0: 1+0j, 1: 0+0j } # それぞれ配列のキーと値の組み合わせは 0 になる確率と 1 になる確率を表す。また値は複素数である。

例えば先ほどでてきた、\( \displaystyle \ket{\psi} = \frac{1}{\sqrt{2}}\ket{0} + \frac{1}{\sqrt{2}}\ket{1} \)の状態は以下の様に表現できます。

import cmath
class QuantumBit:
  def __init__(self):
    self.state = {0: 1/cmath.sqrt(2) + 0j, 1: 1/cmath.sqrt(2) + 0j}

次に「測定」をプログラムで表すと以下の様になります。

import cmath
import random
class QuantumBit:
    def __init__(self):
        self.state = {0: 1/cmath.sqrt(2) + 0j, 1:1/cmath.sqrt(2) + 0j}


    def measure(self): # 測定
        rand = random.random()
        prob = abs(self.state[0] ** 2) # 0 になる確率を算出
        if prob > rand: # 0になる確率を引き当てた場合
          　# 状態を|0>にする
            self.state = {0: 1 + 0j, 1: 0 + 0j}
            # 測定結果 0 をvalueに格納する
            self.value = 0
        else: # 1になる確率を引き当てた場合
            # 状態を|1>にする
            self.state = {0: 0 + 0j, 1: 1 + 0j}
            # 測定結果 1 をvalueに格納する
            self.value = 1

最初 \( \displaystyle \ket{\psi} = \frac{1}{\sqrt{2}}\ket{0} + \frac{1}{\sqrt{2}}\ket{1} \)の状態であった量子ビットを測定することで、ビットの値が 0 か 1 を確定させています。

このように、量子ビットは 0 でも 1 でもない状態をとることができ、測定して初めて 0 か 1 か決まるビットです。

量子ゲート

次に、量子ゲートについて説明していきます。

量子ゲートは論理回路と同様に、ビットに対して影響を与える操作です。

例えば古典コンピュータにおける NOT 回路は 0 を 1 に、1 を 0 に反転させる回路ですが、量子コンピュータでは X ゲートや Y ゲートといったゲートが NOT 回路と近い意味合いを持った量子ゲートになります。

X ゲートや Y ゲートは \( \ket{0} \) を \( \ket{1} \) に、 \( \ket{1} \) を \( \ket{0} \)に変化させます。

量子ゲートには X ゲートや Y ゲート以外にも様々なゲートがありますが、いずれも量子の状態に変化をもたらします。詳細は次に説明するブロッホ球を踏まえて説明します。

ブロッホ球

ここまでで量子ビットと量子ゲートについて説明しましたが、具体的にイメージできる人は多くないと思います。 そこで、量子ビットに量子ゲートを適用したときの変化をイメージしやすく表現できるブロッホ球を紹介します。

まずブロッホ球とは以下のような球のことです。

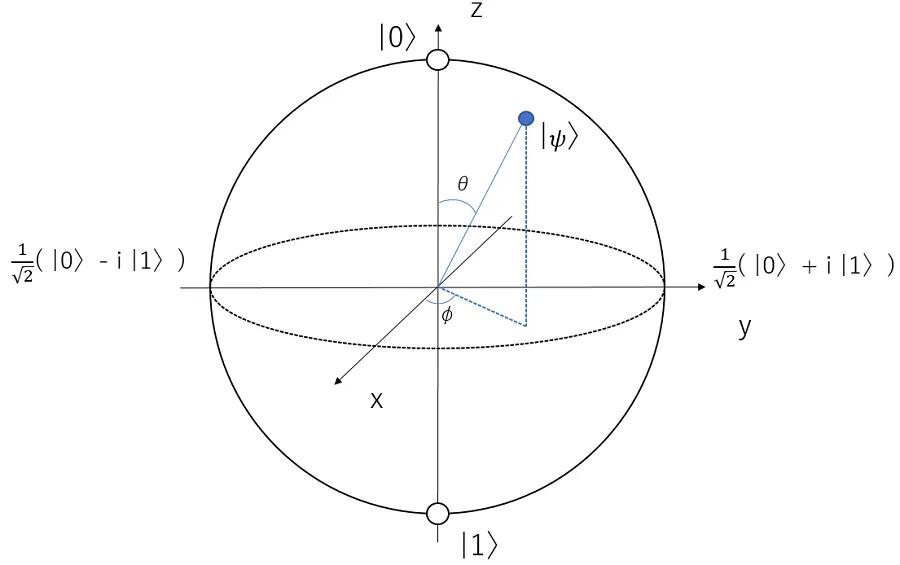
bloch

\(\ket{\psi}\) の位置が量子ビットの状態を表現しており、 \(\ket{\psi} \) はブロッホ球の表面上を移動します。

\(\theta\) と \(\phi\) (ファイ)はそれぞれ、z 軸、x 軸との成す角度を表し、\(\ket{\psi}\)のとる位置によって量子が 0 になる確率と 1 になる確率が決まってきます。

ここで、先ほど量子ビットは(1)式\(\ket{\psi} = \alpha\ket{0} + \beta\ket{1}\)のように表現できるといいましたが、以下(2)式で表すこともできます。 (詳細は省きます)

$$ \ket{\psi} = \cos\frac{\theta}{2}\ket{0} + e^{i\phi}\sin{\frac{\theta}{2}}\ket{1} ・・・(2) $$

この(2)式で表現された量子ビットとブロッホ球を照らし合わせてみます。

例えば、\(\ket{\psi} = \ket{0}\)の場合にはどうなるでしょうか。

\(\ket{\psi} = \ket{0}\)の時、ブロッホ球を見ると\(\theta,\phi\)がそれぞれ 0 になることがわかります。これを(2)式に代入してみると

$$ \begin{align} \ket{\psi} &= \cos\frac{\theta}{2}\ket{0} + e^{i\phi}\sin\frac{\theta}{2}\ket{1} \\ &=\cos{0}\ket{0} + e^{0}\sin{0}\ket{1} \\ &=1\ket{0} + 0\ket{1} \end{align} $$

となり、実際に\(\ket{\psi} = \ket{0}\)であることがわかります。

では、\(\ket{\psi} = \ket{1}\)のときはどうでしょうか。

ブロッホ球を見ると、\(\theta = \pi,\phi = 0\)であることがわかります。これを(2)式に代入してみると

$$ \begin{align} \ket{\psi} &= \cos\frac{\theta}{2}\ket{0} + e^{i\phi}\sin\frac{\theta}{2}\ket{1} \\ &= \cos\frac{\pi}{2}\ket{0} + e^0\sin\frac{\pi}{2}\ket{1} \\ &= 0\ket{0} + 1\ket{1} \end{align} $$

となり、実際に\(\ket{1}\)であることがわかります。

次に、\(\displaystyle \ket{\psi} = \frac{1}{\sqrt{2}}(\ket{0} + \ket{1})\)の時を考えてみます。

$$ \begin{align} \ket{\psi} &= \frac{1}{\sqrt{2}}(\ket{0} + \ket{1}) \\ &= \frac{1}{\sqrt{2}}\ket{0} + \frac{1}{\sqrt{2}}\ket{1} \end{align} $$

となり、(2)式と比較してみると、\(\displaystyle \cos\frac{\theta}{2}=\frac{1}{\sqrt{2}},e^{i\phi}\sin{\frac{\theta}{2}} = \frac{1}{\sqrt{2}}\)になることがわかります。

この 2 条件を満たす\(\theta,\phi\)の組み合わせは、\(\displaystyle\theta = \frac{\pi}{2}, \phi=0\)です。

ブロッホ球で見てみると、以下のようになります。

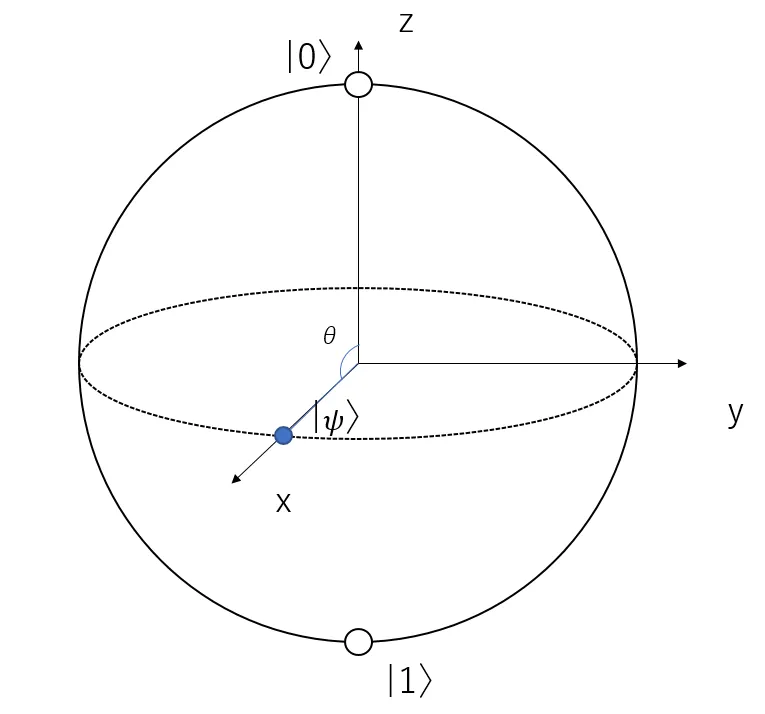
H-bloch

次に、量子ゲートが量子ビットに影響を与える様子をブロッホ球で見ていきます。

まずは以下の図を見てみてください。

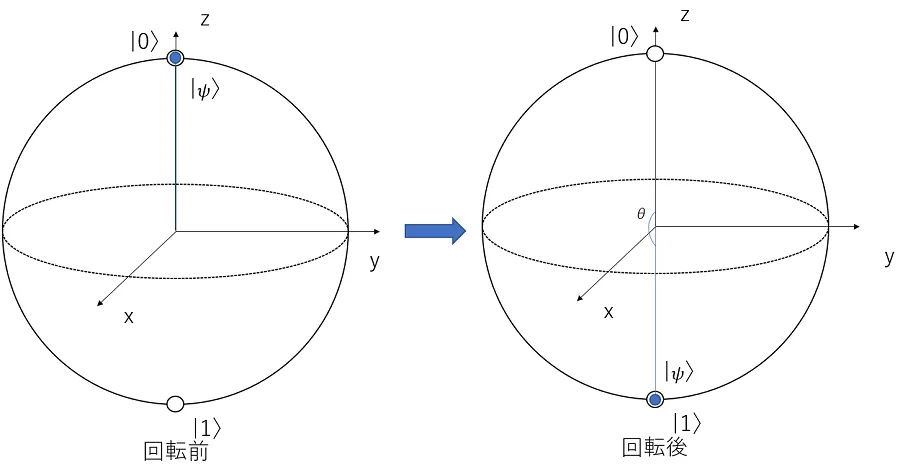
bloch

両者の \(\ket{\psi}\)の位置を見比べてみると、x 軸もしくは y 軸のまわりに 180° 回転させれば\(\ket{0}\)が\(\ket{1}\)になることがわかります。

このことから X ゲートは x 軸のまわりに 180°、Y ゲートは y 軸のまわりに 180° 回転させる量子ゲートと考えることができます。

他にも Z ゲート、H ゲートなどの様々な量子ゲートがありますが全てブロッホ球上の回転で表現することができます。

ここでは今回実装する基本的な量子ゲートと、それらゲートがどのように回転させるのかを紹介します。

X ゲート

x 軸の周りに 180° 回転させる

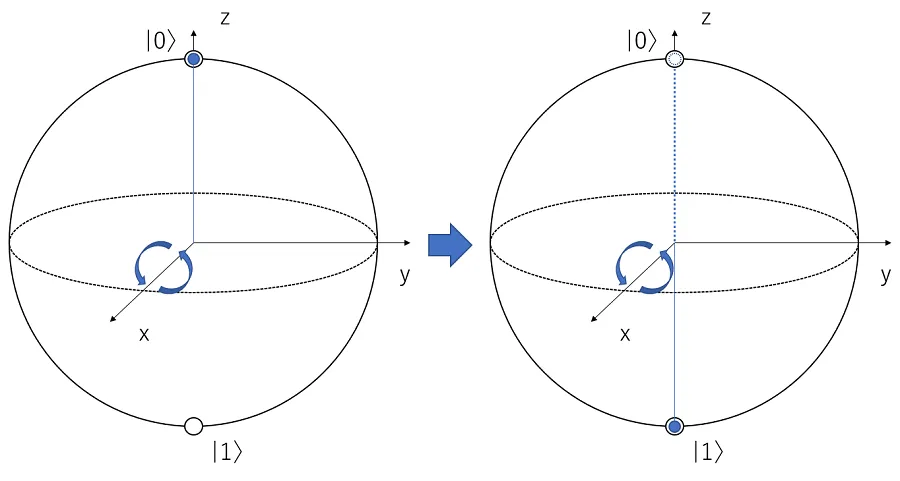
x_gate

Y ゲート

y 軸の周りに 180° 回転させる

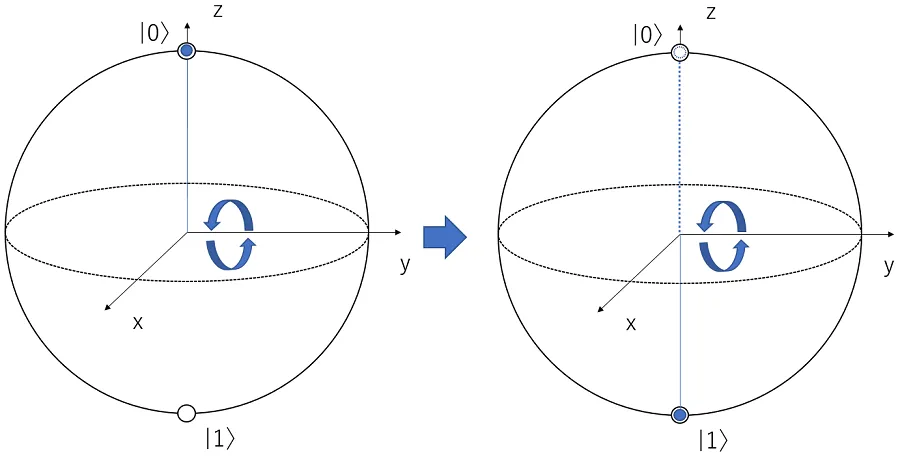
y_gate

Z ゲート

z 軸の周りに 180° 回転させる

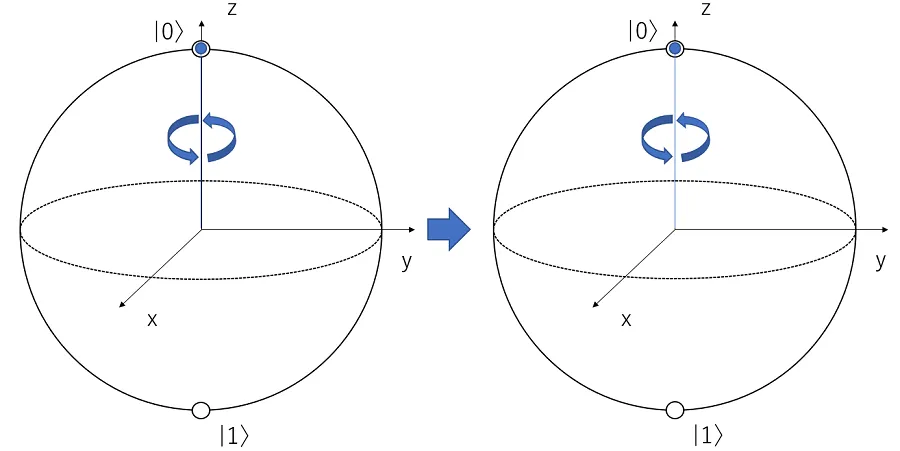
z_gate

Z ゲートは回転前後に変化がないように見えますが、これは\(\ket{0}\)の状態で Z 軸の周りに回転させているからです。 \(\ket{0}\)または\(\ket{1}\)ではない状態に適用すれば変化が起きます。

H(アダマール) ゲート

z 軸から x 軸へと向かう中間の 45° を軸に 180° 回転させる。

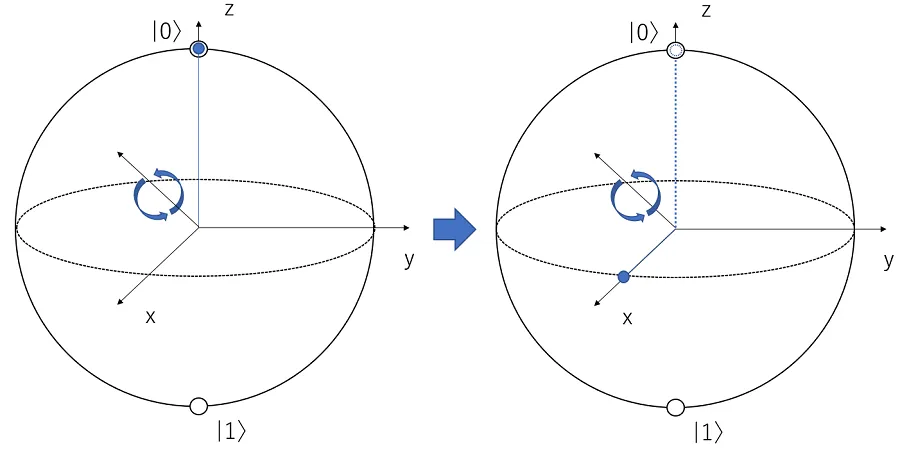
h_gate

図のように\(\ket{0}\) に H ゲートを適用すると \(\frac{1}{ \sqrt{2} }(\ket{0} + \ket{1})\) になります。

量子ゲートの量子ビットへの適用

ここまでで、量子ビットと量子ゲートについて説明しましたが、量子ビットの性質や量子ゲートによる回転といった要素をいまいちどのように実装するのか想像できていない人がほとんどだと思います。

いままで説明した量子ビットや、量子ゲートは行列で表すことができるのでそれを利用します。行列で表すことで、行列の掛け算で量子ビットに量子ゲートを適用させる操作を数学的に計算することができます。

1 量子ビットの行列

まず、1 量子ビット\(\ket{\psi}\)は 2×1 の行列で表します。

$$ \ket{\psi} = \begin{pmatrix} \alpha \\ \beta \end{pmatrix} $$

量子ビットが\(|\alpha|^2\)の確率で\(\ket{0}\)になり、\(|\beta|^2\)の確率で\(\ket{1}\)になる状態を表します。 つまり、\(\ket{0} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} , \ket{1} = \begin{pmatrix} 0 \\ 1 \end{pmatrix}\)です。

class QuantumBit:
  def __init__(self):
    self.state = {0: 1 + 0j, 1: 0 + 0j}
    # state[0]は1行目、state[1]は2行目と考える

量子ゲートの行列

次に量子ゲートですが、今回実装するゲートは 2×2 の行列で表すことができます。

X ゲート

\( \begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix} \)

Y ゲート

\( \begin{pmatrix} 0 & -i\\ i & 0 \end{pmatrix} \)

Z ゲート

\( \begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix} \)

H ゲート

\( \displaystyle \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1\\ 1 & -1 \end{pmatrix} \)

これら量子ゲートの行列をプログラムで表現すると以下のようになります。

# 2x2 の行列を 2x2 の配列で定義する
GATE_X = [[0, 1],[1, 0]]


GATE_Y = [[0, 0-1j], [0+1j, 0]]


GATE_Z = [[1, 0], [0, -1]]


GATE_H = [[1/cmath.sqrt(2), 1/cmath.sqrt(2)], [1/cmath.sqrt(2), -1/cmath.sqrt(2)]]

これら量子ゲートはこういう行列だと覚えるだけで十分ですが、なぜこのような行列になるのか気になる人は以下の詳細を見てみてください。

先ほど量子ゲートはブロッホ球表面上の回転で考えることができるといいました。なので、量子ゲートは回転を表す回転行列と呼ばれる行列を用いて導くことができます。

x,y,z軸それぞれでの回転を表す行列は以下です。

x軸での回転

$$ R_x(\theta) = \begin{pmatrix} \cos{\frac{\theta}{2}} & -i\sin{\frac{\theta}{2}} \\ -i\sin{\frac{\theta}{2}} & \cos{\frac{\theta}{2}} \end{pmatrix} $$

Y軸の回転

$$ R_y(\theta) = \begin{pmatrix} \cos{\frac{\theta}{2}} & -\sin{\frac{\theta}{2}} \\ \sin{\frac{\theta}{2}} & \cos{\frac{\theta}{2}} \end{pmatrix} $$

Z軸の回転

$$ R_z(\theta) = \begin{pmatrix} e^{-i\frac{\theta}{2}} & 0 \\ 0 & e^{i\frac{\theta}{2}} \end{pmatrix} $$

例えば、X ゲートはX軸で180°(\( \pi \))回転させるので、以下のような行列になります。

$$ \begin{align} R_x(\pi) &= \begin{pmatrix} \cos{\frac{\pi}{2}} & -i\sin{\frac{\pi}{2}} \\ -i\sin{\frac{\pi}{2}} & \cos{\frac{\pi}{2}} \end{pmatrix} \\ &= \begin{pmatrix} 0 & -i \\ -i & 0 \end{pmatrix} \\ \end{align} $$

ここで、「グローバル位相」という概念がでてきます。

簡単に言うと、量子全体の位相にズレがでるためそのズレを補正する必要があります。以下で定義される係数をかけることで補正することができます。

$$ e^{i\frac{\theta}{2}} $$

係数のようなものをかけてしまっては、測定に影響がでるのではないか？と思うかもしれませんが、実は影響がでません。

例えば、量子ビット\(\ket{\psi} = 0\ket{0} + i\ket{1}\)を測定すると、\(|i|^2 = 1\)で100%の確率で 1 になります。

この量子ビット\(\ket{\psi} = 0\ket{0} + i\ket{1}\)に\(i\)をかけてみると\(i\ket{\psi} = i*0\ket{0} + i^2\ket{1}\)になりますが、測定結果としては\(|i^2|^2 = |-1|^2 = 1\)なので100%の確率で 1 になることは変わりません。

それらを踏まえて、先ほど\(R_x = \begin{pmatrix} 0 & -i \\ -i & 0 \end{pmatrix} \)と導きましたが、回転を表すこの行列に \(\displaystyle e^{i\frac{\pi}{2}} = cos\frac{\pi}{2} + i\sin{\frac{\pi}{2}} = i\) をかけてみると $$ \begin{align}i(R_x) &= i\begin{pmatrix} 0 & -i \\ -i & 0 \end{pmatrix} \\ &= \begin{pmatrix} 0*i & -i*i \\ -i*i & 0*i \end{pmatrix} \\ &= \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \end{align} $$

になり、前述した Xゲートを導くことができました。

Y ゲートや Z ゲートなども上記のように回転行列に角度を指定したのちに、グローバル位相のズレを係数で補正することで導くことができます。

量子ビットへの適用

次に、量子ゲートを使って回転させる(=量子ビットにゲートを適用する)には、量子ゲートを表す行列と量子ビットを表す行列を掛け算します。

量子ビット \(\ket{0}=\begin{pmatrix} 1 \\ 0 \end{pmatrix}\)と、X ゲートを表す行列\(\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\)を掛け算してみると \(\ket{1}=\begin{pmatrix} 0\\ 1 \end{pmatrix} \) になるはずです。

実際に計算してみると

$$ \begin{align} \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} &=\begin{pmatrix} 0*1+1*0 \\ 1*1+0*0 \end{pmatrix} \\ &=\begin{pmatrix} 0 \\ 1 \end{pmatrix} \end{align} $$

になり、実際に \(\ket{0}\)が\(\ket{1}\)に変わりました。

ここで行列同士の掛け算するときに注意することとして、量子ゲートの行列に量子ビットの行列をかける必要があります。(量子ゲートの行列が左側に来ます)

X ゲート以外もこのように行列の掛け算をすることで、量子ビットにゲートを適用することができます。

これをプログラムにしてみます。

GATE_X = [[0, 1],[1, 0]]
GATE_Y = [[0, 0-1j],[0+1j, 0]]
GATE_Z = [[1, 0], [0, -1]]
GATE_H = [[1/cmath.sqrt(2), 1/cmath.sqrt(2)], [1/cmath.sqrt(2), -1/cmath.sqrt(2)]]


class QuantumBit:
  def __init__(self):
    self.state = {0: 1 + 0j, 1: 0 + 0j}


  # ゲートを適用する
  def _ope_1bit(self, gate):
    res = {}
    # 行列の掛け算をする
    res[0] = gate[0][0] * self.state[0] + gate[0][1] * self.state[1]
    res[1] = gate[1][0] * self.state[0] + gate[1][1] * self.state[1]


    self.state = res


  def x(self):
    self._ope_1bit(GATE_X)


  def y(self):
    self._ope_1bit(GATE_Y)


  def z(self):
    self._ope_1bit(GATE_Z)


  def h(self):
    self._ope_1bit(GATE_H)


# QuantumBitクラスの使用
quantum_bit = QuantumBit()
# 例) xゲートの適用
quantum_bit.x()

プログラム上でも行列の掛け算相当の処理を記述することで、量子ビットに量子ゲートを適用させることができました。

さいごに

今回は1つの量子ビットに着目して量子ビットの重ね合わせや測定、量子ビットへの量子ゲートの適用を実装しました。

ここまでのソースコードをまとめると、以下のようになりました。

import cmath
import random


GATE_X = [[0, 1],[1, 0]]
GATE_Y = [[0, 0-1j], [0+1j, 0]]
GATE_Z = [[1, 0], [0, -1]]
GATE_H = [[1/cmath.sqrt(2), 1/cmath.sqrt(2)], [1/cmath.sqrt(2), -1/cmath.sqrt(2)]]


class QuantumBit:
    def __init__(self):
        self.state = {0: 1 + 0j, 1: 0 + 0j}


    # 測定
    def measure(self):
        rand = random.random()
        prob = abs(self.state[0] ** 2)
        if prob > rand:
            self.state = {0: 1 + 0j, 1: 0 + 0j}
            self.value = 0
        else:
            self.state = {0: 0 + 0j, 1: 1 + 0j}
            self.value = 1


    # ビットへのゲート適用
    def _ope_1bit(self, gate):
      res = {}
      # 行列の掛け算をする
      res[0] = gate[0][0] * self.state[0] + gate[0][1] * self.state[1]
      res[1] = gate[1][0] * self.state[0] + gate[1][1] * self.state[1]


      self.state = res


    def x(self):
      self._ope_1bit(GATE_X)


    def y(self):
      self._ope_1bit(GATE_Y)


    def z(self):
      self._ope_1bit(GATE_Z)


    def h(self):
      self._ope_1bit(GATE_H)

「あれ？思ってたより簡単に実装できている」と感じた人もいるかもしれません。

しかしそれは、1量子ビットのみを実装したからです。複数の量子ビットを扱えるように実装する場合、量子特有の「量子もつれ」という現象を理解する必要があります。

次回は「量子もつれ」という現象を考慮して複数の量子ビットを扱えるように実装していきたいと思います。

▲
TOP
アルファロゴ 株式会社アルファシステムズは、ITサービス事業を展開しています。このブログでは、技術的な取り組みを紹介しています。X（旧Twitter）で更新通知をしています。
X @techblogalpha