はじめに

「量子コンピュータシミュレータを自作してみた」の第2回ということで、この記事では前回に引き続き量子コンピュータの仕組みを追いながら量子コンピュータシミュレータ・ライブラリをプログラミングするということをやっていきたいと思います(第1回の記事はこちら)。

前回までで1量子ビットにおける量子ゲートの適用や測定を実装しました。 今回は複数量子ビットを扱えるようにシミュレータを改良していきます。

量子もつれ

それでは複数量子ビットを扱うためにまず知らなければならない事象である「量子もつれ」について説明します。

量子もつれとは、重ね合わせ状態にある複数の量子の間に強い結びつきができる現象です。 この強い結びつきができるとどうなるのかというと、強い結びつきを持った量子のうち1つの測定結果が他の量子の測定結果にも影響を与えます。

つまり複数の量子ビットを扱っていると、ある量子ビットが他の量子ビットに依存することがあるということです。

例えば2つの量子ビットがあったとします。このとき、どちらの量子ビットも\(\frac{1}{\sqrt{2}}\ket{0} + \frac{1}{\sqrt{2}}\ket{1} \)のような重ね合わせの状態にあるとします。

この2つの量子ビットに量子もつれが発生していない場合、1つ目の量子ビットの測定結果がどんな値になろうと2つ目の量子ビットは50%の確率で0か1になります。

このとき、2つの量子ビットのとりうる値の組み合わせは00,01,10,11となります。

ではこの2つの量子ビットに量子もつれが発生しているとどうでしょうか。

量子もつれが発生すると、2つ目の量子ビットは「1つ目の量子ビットの測定結果が1なら\(\ket{1}\)、1つ目の量子ビットが0なら\(\ket{0}\)になる」といったような状態になったりします。

すると、2つの量子ビットのとりうる値の組み合わせは00,11のみになります。

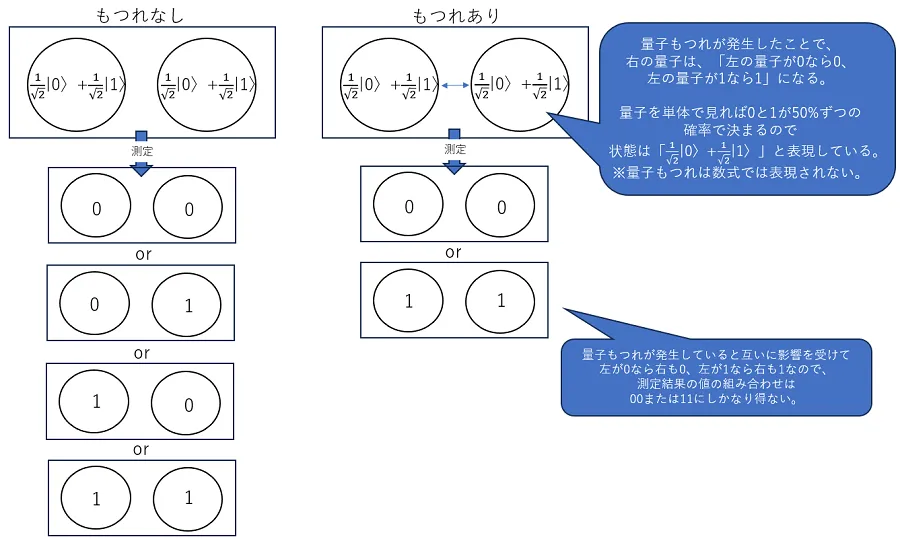
このように量子もつれが発生していると、とある量子ビットの値が他の量子ビットの値に影響されるほか、測定によってとりうる値の組み合わせも変わってきます。

プログラムでの実装における量子もつれ

先ほど量子もつれがどんな現象なのか説明しました。

次に実装の話に入っていきますが、量子もつれが発生している例としてCX(Control X)ゲートがあります。

CXゲートは制御ビット(Control bit)として指定した量子ビットの値が1の場合にのみ、標的ビット(Target bit)として指定した量子ビットにXゲートを適用するゲートです。

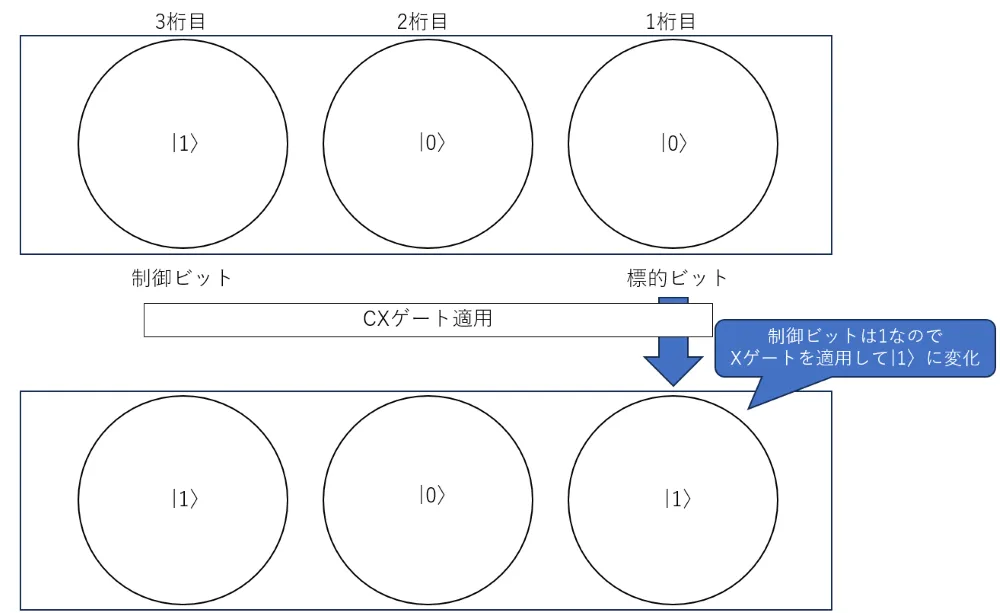
前回作成したプログラムを使って表すと以下のようなイメージです。

import random

GATE_X = [[0,1],[1,0]]
class QuantumBit:
    def __init__(self):
      self.state = { 0: 1+0j, 1: 0+0j }

    def _ope_1bit(self, gate):
      res = {}
      # 行列の掛け算をする
      res[0] = gate[0][0] * self.state[0] + gate[0][1] * self.state[1] 
      res[1] = gate[1][0] * self.state[0] + gate[1][1] * self.state[1] 
    
      self.state = res
    
    def measure(self):
        rand = random.random()
        prob = abs(self.state[0] ** 2)
        if prob > rand:
            self.state = {0: 1 + 0j, 1: 0 + 0j}
            self.value = 0
        else: 
            self.state = {0: 0 + 0j, 1: 1 + 0j}
            self.value = 1
  
    def x(self):
      self._ope_1bit(GATE_X)

    # CXゲートを新たに実装
    def cx(self, control):
        # 制御ビットの値が1ならxゲートを適用
        control.measure()
        if control.value == 1:
            self.x()

quantum_bit1 = QuantumBit()
quantum_bit2 = QuantumBit()

quantum_bit1.cx(quantum_bit2)

上記のように制御ビットの値が1であれば、標的ビットにXゲートを適用するイメージです。

しかし実際にはこんなに単純ではありません。

上記のプログラムでは量子もつれは表現できていますが、とある問題があります。

CXゲート適用時に制御ビットに指定されたビットは測定されてしまい、制御ビットの状態が変化してしまっています。

例えば制御ビットが {0: 0.6+0j, 1: 0.8+0j} の状態だった場合、測定することで それぞれ 36%で 0 に、 64%で 1 に値が確定します。仮に値が0に確定した場合は状態が {0: 1+0j, 1: 0+0j} に変わってしまいます。

このように測定して制御ビットの値を確定をするとその量子ビットは0でも1でもない重ね合わせの状態を失ってしまいます。

そこで複数量子ビットをひとまとめに管理して 制御ビットが 0 でXゲートを適用しなかった場合 と、制御ビットが 1 でXゲートを適用した場合、 両方の確率を状態として持つことで解決します。

イメージ的にはコインの裏表が出る確率をそれぞれ1枚ずつ管理するのではなく、n枚のコインがあったときに1枚目が表で2枚目が裏で・・・というような\(2^n\)通りの組み合わせそれぞれがとりうる確率を管理するイメージです。

複数量子ビット

先ほどまでで、1量子ビットを個別に考えていると測定するまで値が決まらず、CXゲート(量子もつれ)が上手く実装できなそうなことがわかりました。

それを踏まえ、量子ビットを1つずつではなく複数をひとまとめに管理していきます。

前回、1つの量子ビットは以下のように表すことができるとお話ししました。

$$ \alpha\ket{0} + \beta\ket{1} $$

1つの量子ビットは 0, 1 の値をとりうるので上記のように表現しています。

2量子ビットの場合も同様に考えると、 2つの量子ビットの値の組み合わせは 00, 01, 10, 11 の値をとりうるので以下のように表現できます。

$$ \alpha\ket{00} + \beta\ket{01} + \gamma\ket{10} + \delta\ket{11} $$

これは2つの量子ビットの値の組み合わせが\({|\alpha}|^2\)の確率で00、\({|\beta}|^2\)の確率で01、\({|\gamma}|^2\)の確率で10、\({|\delta}|^2\)の確率で11になる状態と解釈できます。

前回は詳細な説明を省きましたが \(\alpha,\beta,\gamma,\delta\)は確率振幅と呼びます。

それぞれ確率振幅を2乗した絶対値がその値になる確率を表し、確率振幅を2乗した絶対値をすべて足し合わせると1になります。

このような複数の量子ビットの状態の扱いをプログラムで表現すると以下のようになります。

また、今回は複雑な行列計算を含む実装を行うためNumPyを使用して配列を作成します。

import numpy
# 複数量子ビット
class QuantumBits:
    def __init__(self, bits_num):
        # 2のbits_num乗の要素数の配列で初期化
        self._state = numpy.array([1 + 0j] + [0 + 0j] * (2 ** bits_num - 1)) 
        # 例えば bits_num=2だと2^2=4要素の配列が作られる。
        # その4つの要素のインデックス「0(00),1(01),2(10),3(11)」はそれぞれ2量子ビットの組み合わせを表し、それぞれの値には量子ビットの組み合わせに対する確率振幅を持つ。

ここまでで複数の量子ビットの状態を同時に管理するためのデータ構造を説明しましたが、実際に量子もつれは考慮できているのでしょうか。

2つの量子ビットがもつれを起こしたときの量子ビットの状態の変化を具体的に考えてみます。

\(\frac{1}{\sqrt{2}} \ket{00} + \frac{1}{\sqrt{2}} \ket{01}\)で1桁目がそれぞれ50%の確率で0か1になる状態に対して、1桁目を制御ビット、2桁目を標的ビットとするCXゲートを適用したときのstateは以下のようになります。

quantum_bits = QuantumBits(2)
quantum_bits._state = [0.7071067811865475+0j, 0.70710678118654757+0j, 0+0j, 0+0j]

# これにCXゲートを適用すると以下に変わる ※まだ実装はしていませんが、実行イメージ
quantum_bits.cx(1,0)
print(quantum_bits._state) 
# [0.7071067811865475+0j, 0+0j, 0+0j, 0.70710678118654757+0j]

これを見てわかることは、それぞれ50%の確率で\(\ket{00}\) か \(\ket{01}\)になる状態だったのが、CXゲートを適用するとそれぞれ50%の確率で\(\ket{00}\) か \(\ket{11}\)になる状態に変化していて、1桁目が0なら\(\ket{00}\)に、1桁目が1なら\(\ket{11}\)になるということを表現できています。

このように複数の量子ビットを一緒に状態として管理することで、測定せずとも量子もつれを考慮することができます。

複数量子ビットにおけるゲートの適用

前回、1つの量子ビットの場合は { 0: 1+0j, 1: 0+0j } \( = \ket{0}\)を行列\(\begin{pmatrix} 1 \\0 \end{pmatrix}\)と表現し、量子ゲートの行列との積を求めることで量子ゲートを量子ビットに適用していました。

少し難しくなりますが、複数量子ビットの場合でも行列の積で適用することができます。

まずは複数量子ビットを行列で表現します。

例えば3量子ビットstate={0: c000, 1: c001, 2: c010, 3: c011, 4: c100, 5:c101, 6: c110, 7: c111} があったとします(確率振幅は変数としてます)。

これは \( \begin{pmatrix} c000 \\ c001 \\ c010 \\ c011 \\ c100 \\ c101 \\ c110 \\ c111 \end{pmatrix} \)と表すことができます。

この複数量子ビットを表す行列と量子ゲートの行列との積で量子ビットに量子ゲートを適用した結果を求めることができます。

しかし前回紹介したように、量子ゲートは 2 * 2 の行列なので、そのままでは3つの量子ビットを表す 8 * 1 の行列との掛け算をすることができません。

3量子ビットの行列にかける行列を どんな量子ゲートを 何ビット目に適用するかという情報を持った 8 * 8 の行列にしてあげる必要があります。

手順としてはそれぞれの量子ビットに適用するゲートをそれぞれ用意し、それらのテンソル積(※1)を求めて 8 * 8 の行列を作ります。

※1:テンソル積（\(\bigotimes\)）とは左の行列の1要素と右の行列の全ての要素をそれぞれ掛け算し、行列を拡張する演算方法です。

例えば3つの量子ビットがあったとして1,2ビット目にはなにもせず、3ビット目にはXゲートを適用する場合には、何も変化を与えない行列（単位行列と呼ばれます）\(\begin{pmatrix} 1&0 \\ 0&1 \end{pmatrix}\)を2つ、Xゲート\(\begin{pmatrix} 0&1 \\ 1&0 \end{pmatrix}\)を1つ用意します。

そして、この3つのテンソル積を求めます。

$$ \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \bigotimes \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \bigotimes \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ \end{pmatrix} $$

ここで注意するのが演算の順番です。

各 2 * 2 の行列の位置に着目して、右から数えて1番目が1ビット目に適用したい行列、2番目が2ビット目に適用したい行列、3番目が3ビット目に適用したい行列になるようにします。

これで 8 * 8 の行列が完成しました。

あとはこの8 * 8の行列と状態を表す行列との積を求めることで、ゲートを適用することができます。

では実際に先ほど求めた 8 * 8 の「3ビット目にXゲートを適用する」行列と \(\ket{000}=\begin{pmatrix} 1 \\ 0 \\ 0 \\0 \\0 \\0 \\0 \\0\end{pmatrix}\) の状態の行列との積を求めてみます。

結果は3ビット目を反転させて\(\ket{100} = \begin{pmatrix} 0 \\ 0 \\ 0 \\0 \\1 \\0 \\0 \\0\end{pmatrix}\)になるはずです。

$$ \begin{pmatrix} 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ \end{pmatrix} \begin{pmatrix} 1 \\ 0 \\ 0 \\0 \\0 \\0 \\0 \\0 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \\0 \\1 \\0 \\0 \\0\end{pmatrix} $$

計算してみると想定通りに変化しました。

ではこれらをプログラムにしてみます。

import cmath
import numpy

# Xゲート
GATE_X = [[0,1], [1,0]]
# 単位行列
MATRIX_ID = [[1+0j ,0+0j], [0+0j, 1+0j]]

class QuantumBits:
    def __init__(self, bits_num):
        # 2のbits_num乗の要素数の配列で初期化
        self._state = numpy.array([1 + 0j] + [0 + 0j] * (2 ** bits_num - 1))        
        self._bits_num = bits_num


    # ゲートを適用するための行列を作成し、stateとの積を求めて量子ゲートを適用する
    def _apply_gate(self, gate, target):
        # 単位行列をbits_num分用意
        matrix = numpy.array([MATRIX_ID] * self._bits_num)
        # 標的ビットに対応する箇所をゲートに置き換える
        matrix[target] = gate
        # bits_num個の行列のテンソル積を求める
        matrix_ope = self._make_matrix(matrix)
        # 行列の掛け算をする
        self._state = matrix_ope @ self._state

        return self

    # 与えられた行列のテンソル積を求める
    def _make_matrix(self, gates):
        res = gates[0]
        for gate in gates[1:]:
            res = numpy.kron(gate, res)
        return res

    def x(self, target):
        self._apply_gate(GATE_X, target)
        return self

    def debug_print(self):
        print(self._state)
        return self


# 3量子ビットを作成
quantum_bits = QuantumBits(3)

# [0j, 0j, 0j, 0j, 1+0j, 0j, 0j, 0j]になる
quantum_bits.x(2).debug_print()

これで複数量子ビットを管理している状態で、特定の量子ビットに量子ゲートを適用することができました。

次に、CXゲートを実装します。

先ほど「2つの単位行列と量子ゲートの行列のテンソル積」と「状態を表す行列」との積でゲートを適用しましたが、CXゲートの場合も同様に行列の積でゲートを適用します。

しかしCXゲートは制御ビットが0の場合と1の場合で標的ビットに量子ゲートを適用するかが変わるので「制御ビットが0の場合何もしない」、「制御ビットが1の場合標的ビットに量子ゲートを適用する」を考える必要があります。

具体的には、「制御ビットが0で何も変化させない行列」と「制御ビットが1で量子ゲートを適用する行列」を作成し、両方を適用させます(状態を表す行列に前述の2つの行列両方を適用する場合、2つの行列を足し合わせた行列と状態を表す行列との積を求めます)。

例えば、1量子ビット目を制御ビット、3量子ビット目を標的ビットにした場合、制御ビットが0の場合と1の場合はぞれぞれ以下のようになります。

【制御ビットが0で何も変化させない行列】 $$ \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \bigotimes \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \bigotimes \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix} $$

3量子ビット目は何も変化させないので対応する行列は単位行列です。

また、制御ビット部分は\( \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}\)となっていますが、これが「対象ビットが0の状態」（0の場合）という意味を持っています。

【制御ビットが1で量子ゲートを適用する行列】 $$ \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \bigotimes \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \bigotimes \begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ \end{pmatrix} $$

3量子ビット目はゲートを適用するので対応する行列はXゲート\(\begin{pmatrix} 0&1 \\ 1&0 \end{pmatrix}\)になっています。

また、制御ビット部分は\( \begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix}\)になっていますが、これが「対象ビットが1の状態」（1の場合）という意味を持っています。

次に、これらの行列を足し合わせます。

$$ \begin{align} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix} + \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ \end{pmatrix} \\ =\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ \end{pmatrix} \end{align} $$

こうしてできた 8 * 8 の行列と状態の行列との積を求めることで、1量子ビット目を制御ビット、3量子ビット目を標的ビットとしたCXゲートを適用することができます。

結果がわかりやすいように、制御ビット以外が0で制御ビットが0と1になる確率がそれぞれ50%ずつの状態\(\begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ 0 \\0 \\ 0 \\ 0 \\ 0 \\ 0\end{pmatrix}\)に先ほどの行列をかけてみます。

結果は制御ビットが0のときは\(\ket{000}\)、制御ビットが1のときは\(\ket{101}\)なので\(\begin{pmatrix} \frac{1}{\sqrt{2}} \\ 0 \\ 0 \\0 \\ 0 \\ \frac{1}{\sqrt{2}} \\ 0 \\ 0 \end{pmatrix}\)になるはずです。

$$ \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0\end{pmatrix}= \begin{pmatrix} \frac{1}{\sqrt{2}} \\ 0 \\ 0 \\ 0 \\ 0 \\ \frac{1}{\sqrt{2}} \\ 0 \\ 0\end{pmatrix} $$

計算してみると想定通りに変化しました。

これをプログラムにしてみます。

import cmath
import numpy

# Xゲート
GATE_X = [[0,1], [1,0]]
# Hゲート
GATE_H = [[1/cmath.sqrt(2), 1/cmath.sqrt(2)],[1/cmath.sqrt(2), -1/cmath.sqrt(2)]]
# 単位行列
MATRIX_ID = [[1+0j ,0+0j], [0+0j, 1+0j]]
# 0を表す行列
MATRIX_0 = [[1,0],[0,0]]
# 1を表す行列
MATRIX_1 = [[0,0],[0,1]]

class QuantumBits:
    def __init__(self, bits_num):
        # 2のbits_num乗の要素数の配列で初期化
        self._state = numpy.array([1 + 0j] + [0 + 0j] * (2 ** bits_num - 1))        
        self._bits_num = bits_num

    def _apply_gate(self, gate, target, control=None):
        # 単位行列をbits_num分用意
        matrix = numpy.array([MATRIX_ID] * self._bits_num)
        # 標的ビットに対応する箇所をゲートに置き換える
        matrix[target] = gate
        
        # 制御ビットがある場合
        if control is not None:
            # ビット数分単位行列を準備する
            mat_0 = numpy.array([MATRIX_ID]*self._bits_num)

            # 制御ビットに対応する箇所を0や1を表す行列に置き換える
            mat_0[control] = MATRIX_0
            matrix[control] = MATRIX_1
   
            # 作成したbits_num * bits_numの行列を足す
            matrix_ope = self._make_matrix(mat_0) + self._make_matrix(matrix)
        else:
            matrix_ope = self._make_matrix(matrix)

        # 行列の掛け算をする
        self._state = matrix_ope @ self._state

        return self

    # 与えられた行列のテンソル積を求める
    def _make_matrix(self, gates):
        res = gates[0]
        for gate in gates[1:]:
            res = numpy.kron(gate, res)
        return res

    def cx(self, control, target):
        self._apply_gate(GATE_X, target, control)
        return self
    
    def h(self, target):
        self._apply_gate(GATE_H, target)
        return self

    def debug_print(self):
        print(self._state)
        return self

# 3量子ビットを作成
quantum_bits = QuantumBits(3)

quantum_bits.h(0).cx(0,2).debug_print()
# 50%でそれぞれ000、101になる 
# [0.7071067811865475+0j, 0j, 0j, 0j, 0j, 0.7071067811865475+0j, 0j, 0j]

測定

ここまでで複数量子ビットでの状態の管理、量子もつれを考慮した量子ゲートの適用を実装できました。

最後に複数量子ビットにおける測定を実装します。

全量子ビットを一括で測定する機能と、指定した1量子ビットのみ測定する機能を実装します。

全量子ビットを一括で測定

まず全量子ビットを一括で測定する機能ですが、これは簡単に実装できます。

複数量子ビットを管理している state の各キーと値はそれぞれ量子ビットの組み合わせと、その確率振幅であるため、 state の要素のうち1つを確率で選ぶことで必然的に全量子ビットの値を測定することができます。

また測定すると state も測定結果に合わせて変更する必要があります。

すべての量子ビットの値はstateから選ばれた要素のキーに確定するため、stateから選ばれた要素の値（確率振幅）は1 + 0j になります。

プログラムにすると以下の様になります。

import random

class QuantumBits:

...

    # 全量子ビットを測定する
    def measure_all(self):
        rnd = random.random()
        state = 0
        cnt = 0
        # 確率振幅をもとに_stateから1つ選ぶ
        for num in range(len(self._state)):
            cnt += abs(self._state[num]) ** 2
            if rnd < cnt:
                state = num
                break
        # 選ばれたキー通りに測定結果を格納する
        self._results = numpy.where(1<<numpy.arange(self._bits_num) & state != 0, 1, 0)
        # 状態を更新する(選ばれたキーの値を1+0jに、それ以外は0+0jにする)
        self._state = numpy.where(numpy.arange(len(self._state)) == state, 1+0j, 0+0j)
        
        return self

指定した1量子ビットのみ測定

次に指定した1量子ビットのみ測定する実装です。

指定した1量子ビットのみ測定する場合には、まず全量子ビットを測定するときと同様にstate のうち1つを確率振幅をもとに確率で選びます。

state の中から選ばれた1要素が表す量子ビットの組み合わせに着目し、その状態の指定された量子ビットを測定結果とします。

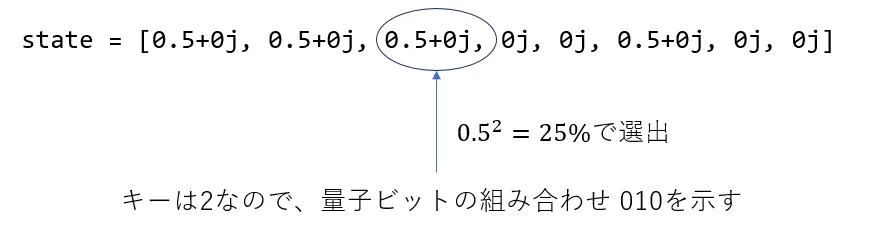
例えば3量子ビット state = [0.5+0j, 0.5+0j, 0j, 0j, 0.5+0j, 0j, 0,5+0j, 0j] において、1量子ビット目を測定するときにインデックス1（2番目）が選出された場合、選出されたstateの要素のキーは1なので、 量子ビットの組み合わせ 001 を表しており、1量子ビット目は1と測定されます。

測定結果はこれだけで出すことができますが、state への影響を考慮していく必要があります。

全ての量子ビットを測定したときと違い、指定した量子ビット以外は測定されていないため、単純に選ばれた state の要素の確率振幅を 1 + 0j にするわけにはいきません。

以下のように state を更新します。

まずは、指定した量子ビットが測定値と一致するstateの要素の確率振幅のみをすべて保持して、新しい state を作ります。例えば、1量子ビット目が1と測定された場合、1量子ビット目が1を表す要素の確率振幅のみ保持します。

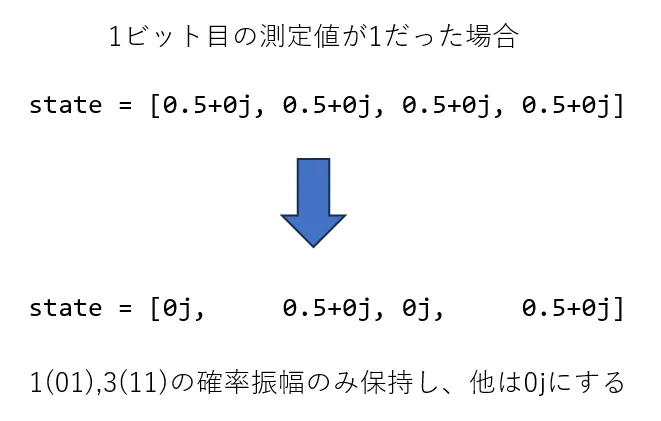
すると、新しく作った state の確率振幅の絶対値の2乗の合計は本来1（100%）になるはずですが1ではなくなってしまっています。

なので各確率振幅に対して、全体の確率の平方根との割合を求めて、各状態の位相を保ったまま確率振幅の絶対値の2乗の合計が1になるように正規化します。

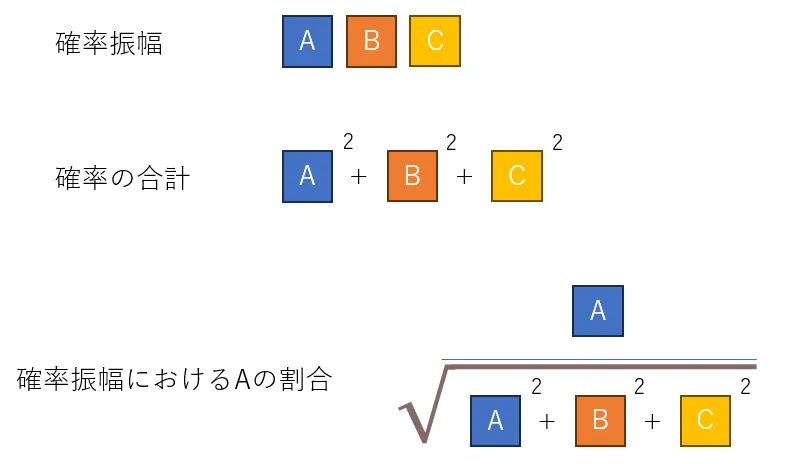
先ほどの3量子ビットと測定結果を元に、stateへの影響を考えてみます。まずは、指定した量子ビット（ここでは1ビット目）が測定値（1）と一致するstateの確率振幅をすべて保持して、新しい state を作ります。

state = [0.5+0j, 0.5+0j, 0j, 0j, 0.5+0j, 0j, 0,5+0j, 0j]のうち、1ビット目が1のキーを持つ state の確率振幅を保持して新しいstateを作ると、 state = [0j, 0.5+0j, 0j, 0j, 0j, 0j, 0j ,0j]となります。

このままだと \(|0.5|^2 = 0.25\)で、合計が1になりませんが、上述のように割合を求めて正規化すると state = [0j, 1+0j, 0j, 0j, 0j, 0j, 0j, 0j] になり、各状態の位相を保ったまま確率振幅の絶対値の2乗の合計値が1になります。

これをプログラムにすると以下のようになります。

class QuantumBits:

...

    # 指定した1量子ビットを測定する
    def measure(self, ix):
        rnd = random.random()
        # 測定結果が0なら0,1ならixビット分1をシフトした値にする
        res_val = 0
        cnt = 0
        # 確率振幅をもとに_stateから1つ選ぶ
        for num in range(len(self._state)):
            cnt += abs(self._state[num]) ** 2
            if rnd < cnt:
                state = num
                break
        
        # 選ばれたキーのixビット目の値を測定結果とする
        if state & 1<<ix != 0:
            res_val = 1<<ix
        self._results[ix] = 1 if res_val else 0
        
        # 状態を更新する
        # 指定ビットが測定結果と一致したときに確率振幅を引き継ぐ
        new_state = numpy.where(numpy.arange(len(self._state)) & 1 <<ix == res_val, self._state, 0)

        # 確率振幅を正規化する
        # 全体の確率を求める(本来1であるべき値がいくつになっているか求める)
        total = numpy.sum(numpy.abs(new_state)**2) + 0j

        # 各確率振幅の値を全体の確率の平方根で割って正規化する
        new_state = new_state / cmath.sqrt(total)
        
        self._state = new_state

        return self

これで複数量子ビットにおいて量子ゲートの適用、測定まで実装することができました。

今までのソースコードをまとめると、以下のようになりました。

import cmath
import random
import numpy

# Xゲート
GATE_X = [[0,1], [1,0]]
# Yゲート
GATE_Y = [[0, 0-1j], [0+1j, 0]]
# Zゲート
GATE_Z = [[1,0],[0,-1]]
# Hゲート
GATE_H = [[1/cmath.sqrt(2), 1/cmath.sqrt(2)],[1/cmath.sqrt(2), -1/cmath.sqrt(2)]]
# 単位行列
MATRIX_ID = [[1+0j ,0+0j], [0+0j, 1+0j]]
# 0を表す行列
MATRIX_0 = [[1,0],[0,0]]
# 1を表す行列
MATRIX_1 = [[0,0],[0,1]]

class QuantumBits:
    def __init__(self, bits_num):
        # 2のbits_num乗の要素数の配列で初期化
        self._state = numpy.array([1 + 0j] + [0 + 0j] * (2 ** bits_num - 1))        
        self._bits_num = bits_num

        # 測定結果格納用
        self._results = numpy.array([None] * bits_num)

    def _apply_gate(self, gate, target, control=None):
        # 単位行列をbits_num分用意
        matrix = numpy.array([MATRIX_ID] * self._bits_num)
        # 標的ビットに対応する箇所をゲートに置き換える
        matrix[target] = gate
        
        # 制御ビットがある場合
        if control is not None:
            # ビット数分単位行列を準備する
            mat_0 = numpy.array([MATRIX_ID]*self._bits_num)

            # 制御ビットに対応する箇所を0や1を表す行列に置き換える
            mat_0[control] = MATRIX_0
            matrix[control] = MATRIX_1
   
            # 作成したbits_num * bits_numの行列を足す
            matrix_ope = self._make_matrix(mat_0) + self._make_matrix(matrix)
        else:
            matrix_ope = self._make_matrix(matrix)

        # 行列の掛け算をする
        self._state = matrix_ope @ self._state

        return self

    # 与えられた行列のテンソル積を求める
    def _make_matrix(self, gates):
        res = gates[0]
        for gate in gates[1:]:
            res = numpy.kron(gate, res)
        return res
    
    # 全量子ビットを測定する
    def measure_all(self):
        rnd = random.random()
        state = 0
        cnt = 0
        # 確率振幅をもとに_stateから1つ選ぶ
        for num in range(len(self._state)):
            cnt += abs(self._state[num]) ** 2
            if rnd < cnt:
                state = num
                break
        # 選ばれたキー通りに測定結果を格納する
        self._results = numpy.where(1<<numpy.arange(self._bits_num) & state != 0, 1, 0)
        # 状態を更新する(選ばれたキーの値を1+0jに、それ以外は0+0jにする)
        self._state = numpy.where(numpy.arange(len(self._state)) == state, 1+0j, 0+0j)
        
        return self
    
    # 指定した1量子ビットを測定する
    def measure(self, ix):
        rnd = random.random()
        # 測定結果が0なら0,1ならixビット分1をシフトした値にする
        res_val = 0
        cnt = 0
        # 確率振幅をもとに_stateから1つ選ぶ
        for num in range(len(self._state)):
            cnt += abs(self._state[num]) ** 2
            if rnd < cnt:
                state = num
                break
        
        # 選ばれたキーのixビット目の値を測定結果とする
        if state & 1<<ix != 0:
            res_val = 1<<ix
        self._results[ix] = 1 if res_val else 0
        
        # 状態を更新する
        # 指定ビットが測定結果と一致したときに確率振幅を引き継ぐ
        new_state = numpy.where(numpy.arange(len(self._state)) & 1 <<ix == res_val, self._state, 0)

        # 確率振幅を正規化する
        # 全体の確率を求める(本来1であるべき値がいくつになっているか求める)
        total = numpy.sum(numpy.abs(new_state)**2) + 0j

        # 各確率振幅の値を全体の確率の平方根で割って正規化する
        new_state = new_state / cmath.sqrt(total)
        
        self._state = new_state

        return self
    
    def x(self, target):
        self._apply_gate(GATE_X, target)
        return self

    def cx(self, control, target):
        self._apply_gate(GATE_X, target, control)
        return self
    
    def y(self, target):
        self._apply_gate(GATE_Y, target)
        return self
        
    def z(self, target):
        self._apply_gate(GATE_Z, target)
        return self
    
    def h(self, target):
        self._apply_gate(GATE_H, target)
        return self

    def debug_print(self):
        print(self._state)
        print(self._results)
        return self

さいごに

いかがでしたでしょうか。

量子コンピュータは難しい物だと思っていましたが、たった80行程度のプログラムである程度の機能を持ったシミュレータライブラリを作れてしまうのかという驚きもあったと思います。

2回にわたって「量子コンピュータシミュレータを自作してみた」と題して書いたブログも今回で終了になります。この記事が皆様の量子コンピュータの理解に役立てば幸いです。ありがとうございました。