はじめに

データを分析し、可視化してわかりやすく示すことができるソフトウェアにはBIツールがあります。Excelのような（データからグラフを作成する）表計算ソフトの高機能版と考えれば分かりやすいです。BIツールではExcelと比べてより幅広いデータ分析・可視化ができます。

BIツールでは「データの分布」を可視化し、カテゴリごとにどのような傾向がみられるかを確認することができます。しかし、カテゴリごとに分けた図示化をする際に注意点があり、フィルタリングの考え方について理解する必要があります。

私自身が経験した課題として、各社員がスキル診断を受診し、そのスコアの一覧が出た際に、社員の年次によってスコアのばらつきがどうなっているかを確認したいという事例がありました。
BIツールのPower BIを用いてスコアのデータを正規分布で図示する分析を行ったのですが、その際、データのフィルタリングの考え方を考慮しなかったために詰まってしまった箇所がありました。
この記事ではその事例をとりあげ、Power BIを用いたデータ分析で注意すべき点について説明します。そうすることでよりスムーズにデータ分析を行えるようになることを目指しています。

今回扱う事例について

今回取り上げる事例は、年次ごとの社員のスコア分布を正規分布を用いて可視化するものです。
BIツールにはマイクロソフト社が提供する「Power BI ⧉」を使用します。
Power BIには有償版もありますが、Microsoft アカウントさえあれば無償で利用することができ、入門としても適しています。

今回、分析対象となるデータには、「社員番号」「年次」「スコア」の3つのカラムがあります。以下の図1はデータから一部の行を抜き出してきたものです。

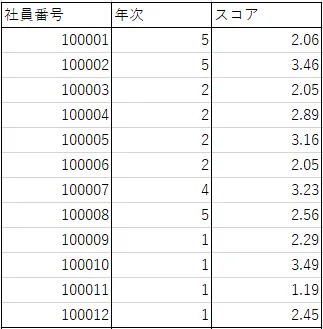
「社員番号」は各社員を表す値で、「年次」は診断を受けた時点での各社員の年次（1年目、2年目、……）を指します。「スコア」は、特定の社員（社員番号：○○○○○○）が特定の年次（年次：×年目）で受けたスキル診断の結果を表します。なお、スコアは0～5までの範囲の値をとるようになっています。
これらのデータをもとに、年次ごとに社員のスコア分布を正規分布曲線で図示化して、表示します。
次いで、歪度を計算することで、実際の分布がその正規分布からどの程度ずれているかを確認します。

スコア分布の図示化では、スコアを横軸に、正規分布の値（確率密度関数）を縦軸に設定した曲線グラフを作成します。
具体的には、0～5までのスコアを0.1のサイズで区切って、そのそれぞれの値について正規分布の値を計算し、それを縦軸に配置します。
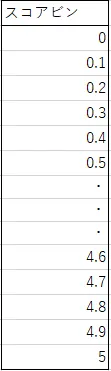
そのために「正規分布表示用」テーブルを別に用意し「スコアビン」カラムを作成しています（図2）。
ビンというのは一般的に、ヒストグラムなどにおいて値をある単位（0.1など）で区切って、同じサイズのグループ（0.3～0.4、0.4～0.5など）に分けて視覚化する際に使われるもので、ここでは「スコア」を「ビン」で分割するイメージで「スコアビン」という名称を使っています。

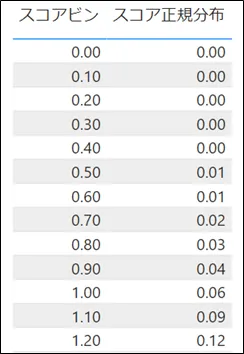
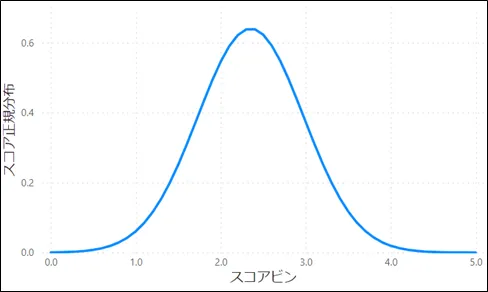
流れとしては、まず図1の「スコア表」のデータおよび図2の「スコアビン」カラムによって正規分布の値を計算します。すると、その結果は図3のようになります。図3では、計算した正規分布の値を「スコア正規分布」というカラム名で表示しています。次いで、この図3の結果を、図4のように曲線の形で表示します。

データ分析の用語について

正規分布、歪度はともにデータ分析のための指標を表す用語です。これらがどういうもので、なぜそれを使うのかについて説明します。

正規分布についての説明

正規分布は最も一般的な分布であり、平均値を中心に、左右対称のベル状の形状をしています。平均値と中央値と最頻値が一致するという特徴を持っています。
データが正規分布に従うことを仮定すれば、データが各値をとる確率も計算できるようになります。
正規分布図はデータのばらつきを確率分布として表現しています。このばらつきを「確率密度」といいます。
正規分布の内側の面積は1となっており、横軸となるパラメータが「ある値以上あるいは以下の範囲」にある確率を求めたい場合、その範囲にある正規分布の内側の面積を求めれば、その面積値が確率になるという特徴があります。
正規分布の値（縦軸）は、横軸となるパラメータの各値について、全体の平均および標準偏差の値をもとに算出しています。

歪度についての説明

データは正規分布に従うことが多いですが、実際の分布がそこからずれているという場合も多くあります。そこで「歪度」の値を計算すれば、データが正規分布からどの程度ずれているかが分かります。
歪度はデータをヒストグラムにしたとき、そのヒストグラムの形がどれだけ正規分布より左右に偏っているかを示す値です。「左に偏った」分布のときには正の値、「右に偏った」分布のときには負の値になります。おおまかなイメージとしては以下の図5～図7のようになります。

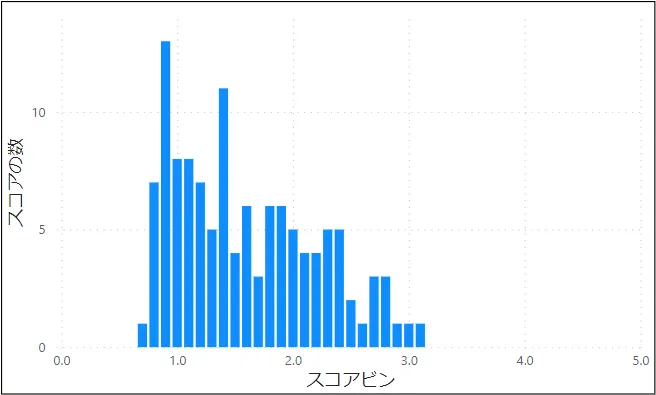
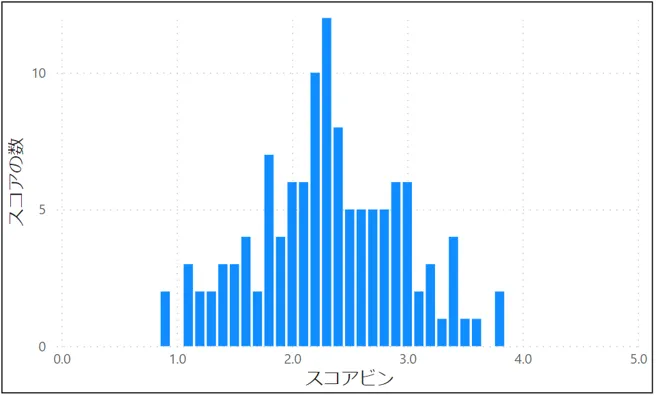
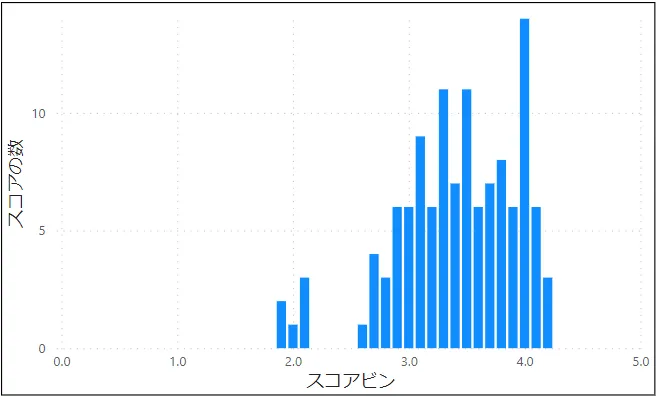
歪度は横軸となるパラメータの各値に加えて全体の平均および標準偏差、そしてデータの個数をもとに算出します。

詰まってしまった点

今回とりあげる事例の概要について前セクションまでで説明しましたが、このセクションでは実際に私がどのような点に詰まってしまったかを説明します。

前提

前提として、Power BIではDAX関数でメジャーを定義して値を算出することができます。「メジャー」というのは、Power BIのテーブル内で定義できるフィールドの一種で、分析対象の集計値（合計、平均など）のことです。
今回の例では「スコア数」「スコア平均」「スコア標準偏差」のメジャーを作成し、計算式を与えて算出しています。それぞれ専用のDAX関数を使用して計算でき、以下のような式になります。

スコア数 = COUNTX('スコア表',[スコア])  
スコア平均 = AVERAGEX('スコア表',[スコア])  
スコア標準偏差 = STDEVX.P('スコア表',[スコア])  

それぞれ、第1引数にテーブル名、第2引数に列名を指定すれば、指定したテーブルのデータを全体と見なし、その列にある値の数、平均、標準偏差を表す数値を返します。

また、正規分布の値についてもNORM.DIST関数を用いて計算できます。一般的に、分布を求めたい値が \( x \) の場合、正規分布は以下のような式で定義されます。

正規分布 = NORM.DIST(x,平均,標準偏差,FALSE)  

※FALSEの部分は関数の形式を決定する論理値であり、NORM.DIST関数ではこの論理値がTRUEの場合は累積分布関数を返し、FALSEの場合は確率密度関数を返します。今回は確率密度関数を求めたいのでFALSEになります。

したがって、今回求める「スコア正規分布」のメジャーは以下の式で計算します。

スコア正規分布 = NORM.DIST(SUM('正規分布表示用'[スコアビン]),[スコア平均],[スコア標準偏差],FALSE)

スコアを0.1単位で分割した「スコアビン」の値ごとに正規分布の値を計算し、曲線で図示化します。

歪度については専用のDAX関数が用意されていないため、ユーザー側で計算式を指定します。
一般に、サンプルサイズを \( n \) 、各データの値を \( x_i \) 、データの平均値を \( \bar x \) 、標準偏差を \( s \) とすると、歪度は次の式から求められます。

$$ 歪度 = \frac{n}{(n-1)(n-2)}\sum_{i=1}^{n}(\frac{x_i - \bar x}{s})^3$$

したがって、今回求める「歪度」のメジャーは以下の式で計算します。

歪度 = [スコア数]/(([スコア数]-1)*([スコア数]-2))*SUMX('スコア表',(([スコア] - [スコア平均])/[スコア標準偏差])^3)

詰まった事象

今回詰まってしまった事象は、「歪度」の値が正しく計算できないということです。
上記の通りに「歪度」の計算式を定め、計算値をビジュアル上に表示しようとしてもエラーになってしまいます（図8）。

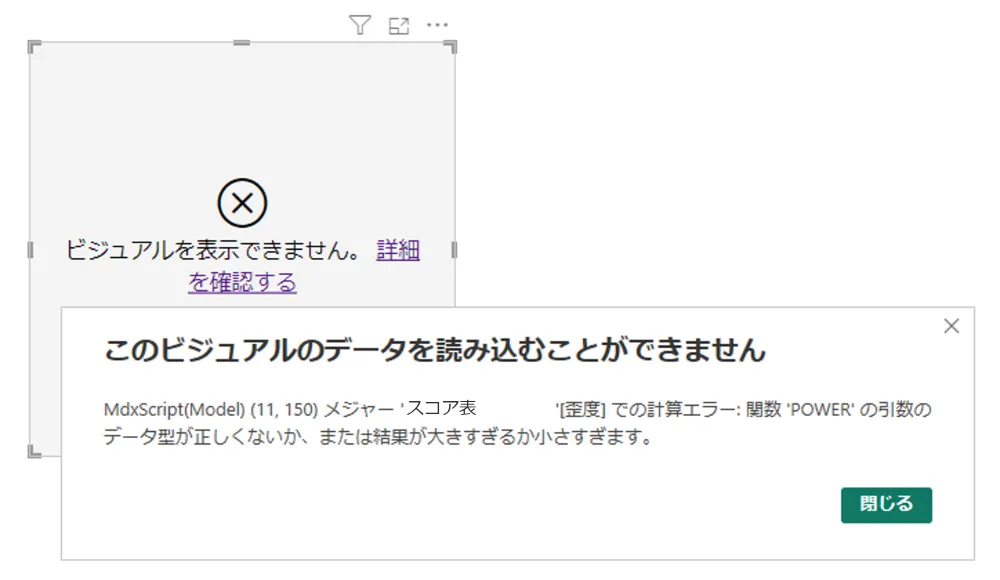
エラーメッセージを見ると、POWER関数（累乗計算）の部分がおかしいと出ていました。したがって、3乗している部分の中、以下の式で誤りが出ていると分かります。なお、データ型については誤りはありませんでした。

([スコア] - [スコア平均]) / [スコア標準偏差]

ここから、計算式に用いている「スコア平均」や「スコア標準偏差」の値に何か間違いがあるということが考えられます。例えば「スコア標準偏差」の値が0になることがあれば、この部分にエラーが出ることになります。
そこで仮説として、各メジャーで参照しているデータの範囲が正しくないために、正しい平均や標準偏差が計算されていない可能性があるということに思い当たり、調査を行いました。

不足していた知識 - フィルタリングの考え方

分かっていなかった点としては、「スコア数」「スコア平均」「スコア標準偏差」など各メジャーを計算する際、参照するデータの範囲がどのように決まっているかがあります。それについて説明するうえで、Power BIのフィルタリングの考え方として「外部的なフィルター」と「内部的なフィルター」という分け方を紹介します。

外部的なフィルターと内部的なフィルターについて

「外部的なフィルター」と「内部的なフィルター」というのは便宜上の言い方ですが、両者の意味について詳しく説明します。

• 外部的なフィルターとは・・・
  • ビジュアル（図表）の外部から行われているフィルタリング
  • スライサー、他ビジュアルでのカテゴリ選択による絞り込みなど、ビジュアルの外部から適用されているフィルター
• 内部的なフィルターとは・・・
  • ビジュアルが内部的に行っているフィルタリング
  • 内部の軸や行・列などで分けられた時系列・カテゴリなど。ビジュアルの内部でカテゴリごとの値を算出する際に適用される。行フィルター・列フィルターとも言う

今回の例では、例えばスライサー（表の外部のフィルター）などで「年次」で「5」を選択した場合、「年次」が「5」のレコードのみが表に存在するようになります。これが「外部的なフィルター」の例です（図9）。

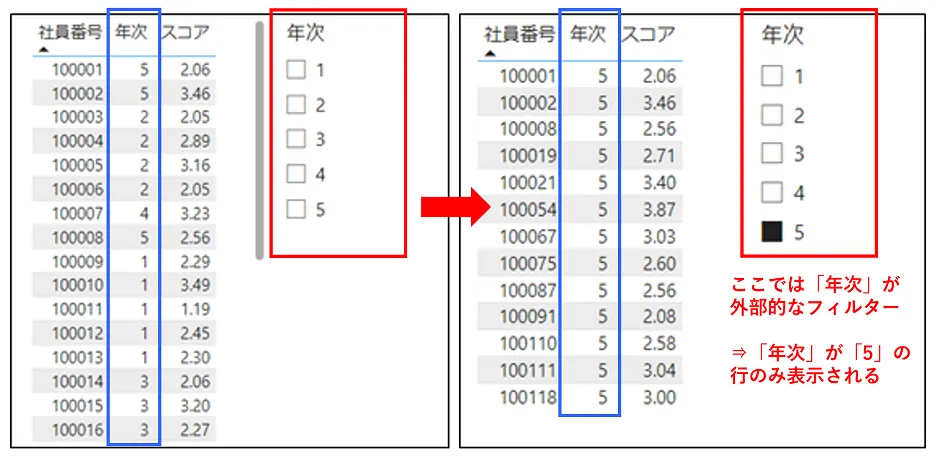
また、「内部的なフィルター」の例としては、「年次」ごとに「スコア」の数や平均値を出していた表において、「社員番号」の列を追加すると、「社員番号」の値ごとに行が分かれて表示されるようになります（図10）。

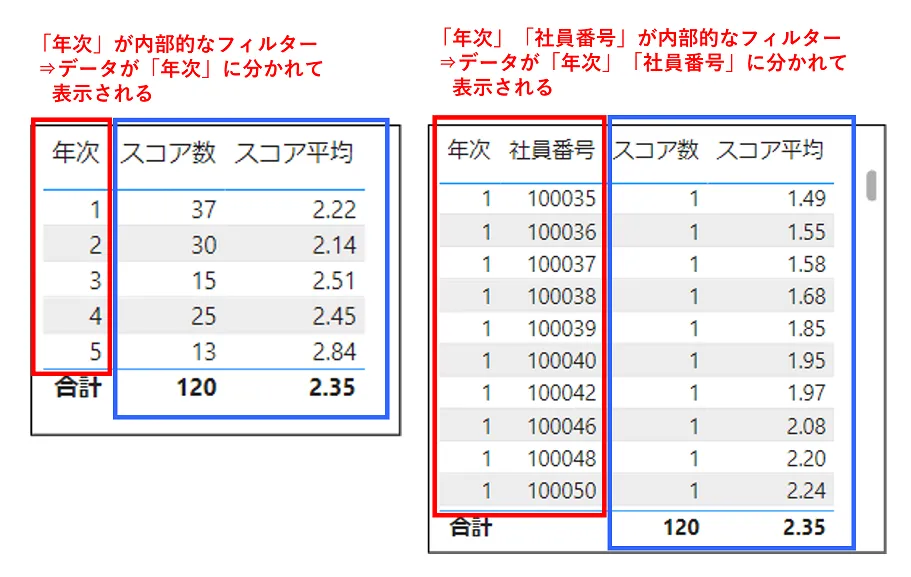
図10の左の表の場合、「スコア平均」の各値の計算に使われているデータは、全てのデータから各「年次」でフィルターされたものです。1行目の場合、「年次」が「1」のデータ全て（37件）から計算されています。
右の表の場合、「スコア平均」の各値の計算に使われているデータは、全てのデータから各「年次」と「社員番号」でフィルターされたものです。1行目の場合、「年次」が「1」でかつ「社員番号」が「100035」のデータだけが抽出され、そのデータ全て（1件）をもとに「スコア平均」の値が計算されています。
この場合の「年次」や「社員番号」といった列が「内部的なフィルター」と呼ばれるものです。

内部的なフィルターだけを除く方法

「外部的なフィルター」と「内部的なフィルター」について説明しました。通常であればPower BIのビジュアルではこの両方のフィルターがともに適用された値が表示されますが、「外部的なフィルターは適用しつつ内部的なフィルターは無視したい」という場合も考えられます。
例えば、「年次」ごとに行が分かれたグラフにおいても、全体のスコア数の値を表示したい、といった場合です。
そういった場合には、計算に使う式のなかでALLSELECTED関数を使用すれば実現できます。たとえば以下のような形です。

スコア数 (通常) = COUNTX('スコア表',[スコア])
スコア数ALLSELECTED = COUNTX( ALLSELECTED('スコア表') ,[スコア])

ALLSELECTED関数を使用するかしないかで計算結果は変わってきます（図11）。

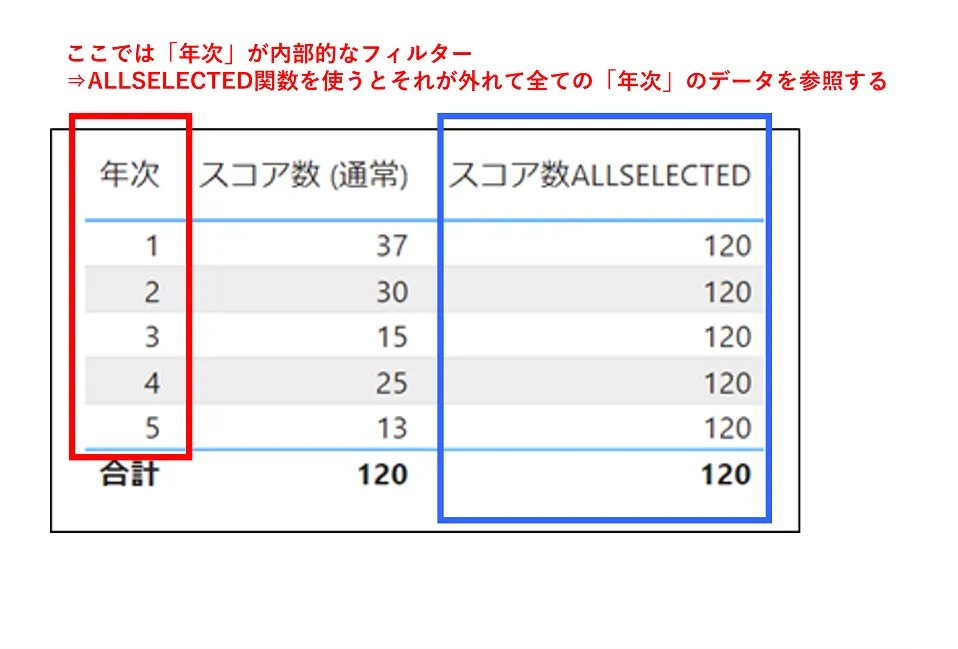
ALLSELECTED関数の引数にテーブル名を指定することで、（「外部的なフィルター」は適用された上で）「内部的なフィルター」に左右されずそのテーブルにあるデータ全体を参照できます。
ちなみに補足として、ALL関数というものもあり、こちらを使用すれば「内部的なフィルター」だけでなく「外部的なフィルター」も無視して、全てのデータを参照します。

どのように解決したか

前セクションでの内容を踏まえたうえで、今回起こっていた問題点について説明します。
「スコア数」「スコア平均」「スコア標準偏差」など各メジャーを計算する際、参照するデータの範囲を把握できていなかったことに問題がありました。「スコア正規分布」の値を計算する場合と、「歪度」の値を計算する場合とでは違う計算式で範囲を指定する必要があります。

正規分布を計算する場合

正規分布の値は、各々の「スコアビン」の値について、以下のような式で算出していました。

スコア正規分布 = NORM.DIST(SUM('正規分布表示用'[スコアビン]),[スコア平均],[スコア標準偏差],FALSE)

ここで用いられる「スコア平均」や「スコア標準偏差」は、「外部的なフィルター」に加えて「内部的なフィルター」（行フィルター・列フィルター）がかかったデータをもとに出しています（図12）。
図12を見ると「年次」が「1」に該当するデータはテーブル全体の120件中の37件あり、「スコア平均」や「スコア標準偏差」ではその37個のスコア値の平均や標準偏差を出しています。

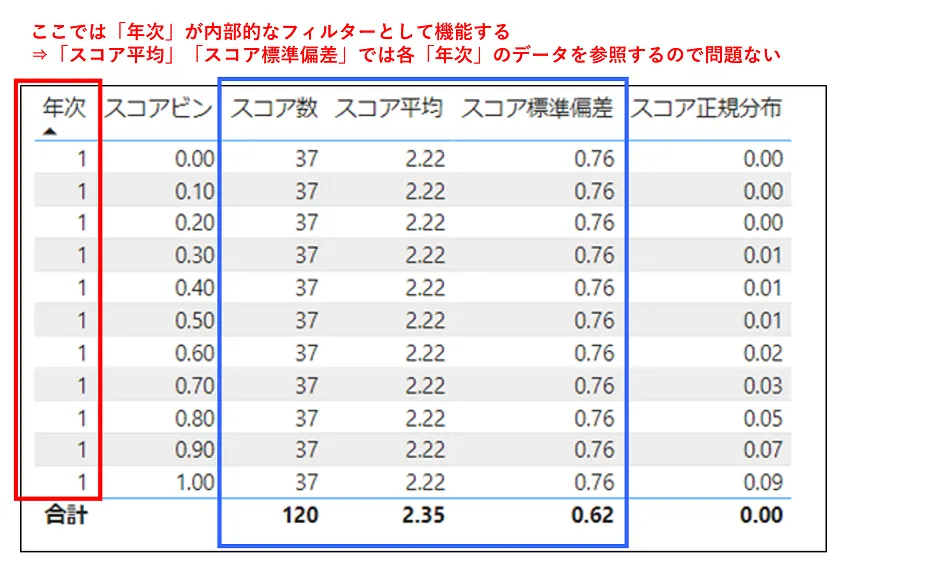
「スコア数」「スコア平均」などの計算式においてALL関数やALLSELECTED関数を用いない場合、「外部的なフィルター」に加えて、「内部的なフィルター」（この場合は「年次」が「1」という条件）がかかったデータを参照して値を計算しています。
「スコア正規分布」の値を出す場合はこれで問題ありません。

歪度を計算する場合

「歪度」を計算する場合、そのなかでの「スコア平均」「スコア標準偏差」は、「スコア正規分布」の値を出す場合とは違う計算式で範囲を指定する必要があります。
以下でそれについて説明します。
「歪度」は以下のような式で算出していました。

歪度 = [スコア数]/(([スコア数]-1)*([スコア数]-2))*SUMX('スコア表',(([スコア] - [スコア平均])/[スコア標準偏差])^3)

この式の前半の[スコア数]/(([スコア数]-1)*([スコア数]-2))と後半のSUMX('スコア表',(([スコア] - [スコア平均])/[スコア標準偏差])^3)とで、フィルターについての扱いが異なっています。
前半にある、「スコア数」を使っている計算部分では個別のスコアの値を考慮しておらず、後半にある、SUMX関数の中の計算部分では個別のスコアの値を考慮しています。
そして、前半部分にある「スコア数」の算出にはALLSELECTED関数を使う必要がなく、後半部分にある「スコア平均」「スコア標準偏差」の算出にはALLSELECTED関数を使う必要があります。

前半にある「スコア数」を使っている計算部分は以下の通りです。

[スコア数]/(([スコア数]-1)*([スコア数]-2))

ここでの「スコア数」に関しては、ALLSELECTED関数を使う必要はなく、通常通り以下のような計算を用います。

スコア数 = COUNTX('スコア表',[スコア])

この「スコア数」の計算のイメージは、以下の図13のようになります。

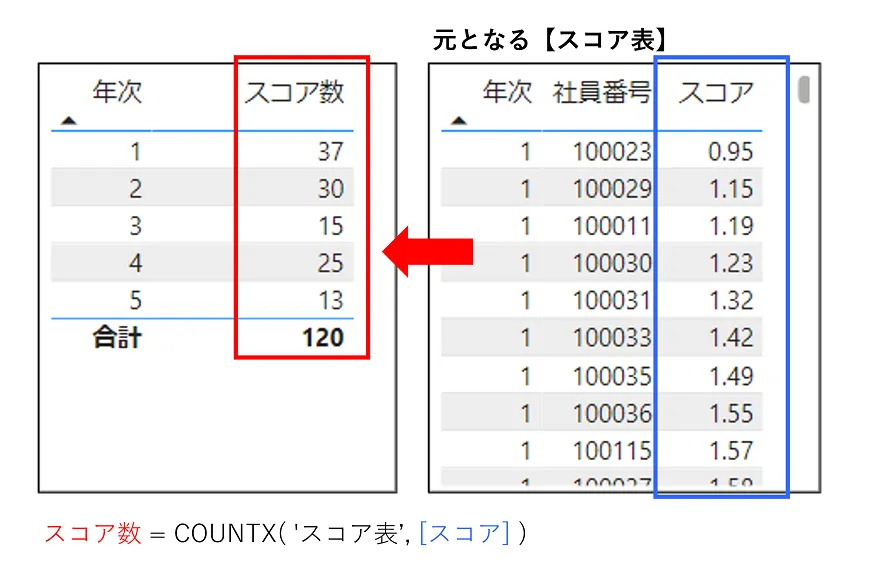
元となる「スコア表」は各「スコア」によって行が分かれていますが、「スコア数」の算出では各「スコア」の値を考慮しないため、左表のように集計する形になります。
この左表では、「年次」が「内部的なフィルター」の役割を持っています。各「年次」によって、元となる「スコア表」のデータがフィルタリングされて、その数が「スコア数」として算出されています。
例えば「年次」が「1」のデータの歪度を計算したい場合、それに該当するデータの件数が37であれば、「スコア数」にはそのまま37を用いるため、「スコア数」の計算ではALLSELECTED関数のような処理を使う必要はありません。

後半のSUMX関数を使っている部分については扱いが異なります。ここではSUMX関数の第2引数で指定した計算式を、すべての「スコア」の値について計算しています。SUMX関数の部分を取り出すと以下の式になります。

SUMX('スコア表',(([スコア] - [スコア平均]) / [スコア標準偏差])^3)

SUMX関数は、第1引数に指定したテーブルの各行について、第2引数の計算を行い、その結果を合計することができる関数です。
「スコア表」は各「スコア」によって行が分かれていて、ここではそのそれぞれの行について、SUMX関数の中の計算を行います。37行あるデータであれば、SUMX()のカッコの中の計算式を37回計算して、その値を合計しているということになります。
Power BIの仕様として、SUMX関数などのイテレータ関数内の式ではフィルターが切り替わる挙動になっています。
そのため、前半の式では「年次」は内部的なフィルターとして機能していましたが、この後半の式では「年次」は外部的なフィルターに変換されており、内部的なフィルターは各行に変わっていることになります。

そして、ここで用いられる「スコア平均」や「スコア標準偏差」は、ALLSELECTED関数を使用し、「外部的なフィルター」（「年次」など）のみがかかったデータを参照して計算する必要があります。
「スコア」によって行が分かれたデータを用いつつも、「スコア平均」や「スコア標準偏差」の値に関しては、各「スコア」の値ではなく、「外部的なフィルター」がかかったデータ全体から算出する必要があるためです。
これについて、今回の事例から具体的に説明します。

今回問題となった事象においては、「スコア平均」や「スコア標準偏差」の値を計算する際にALLSELECTED関数を使っていなかったので、個々の「スコア」の値について平均や標準偏差を計算してしまい、失敗していました（図14を参照）。
今回は「年次」ごとの「歪度」を出したいため、「年次」が「外部的なフィルター」にあたります。図14は「年次」が「1」の場合の歪度を出す場合の計算イメージです。図14の右上側にある「年次」フィルターが「外部的なフィルター」です。
「年次」が「1」に該当するデータは37行あるため、ここで集計対象になるデータ全体の数は37となり、図14の右下側の表を見ると「スコア数」の合計は37になっています。

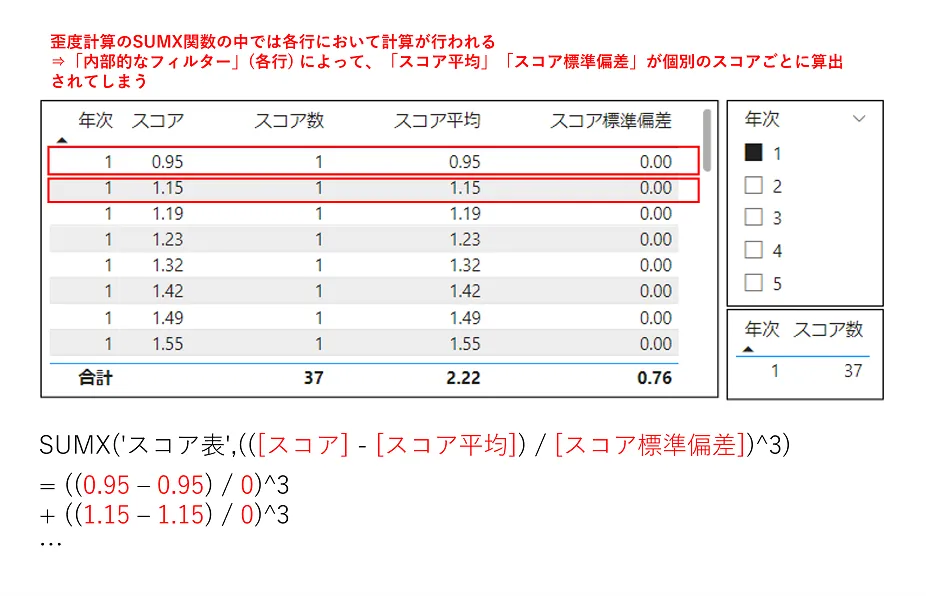
図14の各行において「スコア数」が1となってしまい、「スコア平均」や「スコア標準偏差」の計算において単一の「スコア」の値しか参照していないことになります。そのため、「スコア」と「スコア平均」の値がイコールになり、「スコア標準偏差」の値が0になっています。これが、歪度の値を正しく計算できずエラーになっている原因でした（図15）。

そこで、各メジャー（「スコア平均」「スコア標準偏差」）の計算式においてALLSELECTED関数を使用するように変更しました。

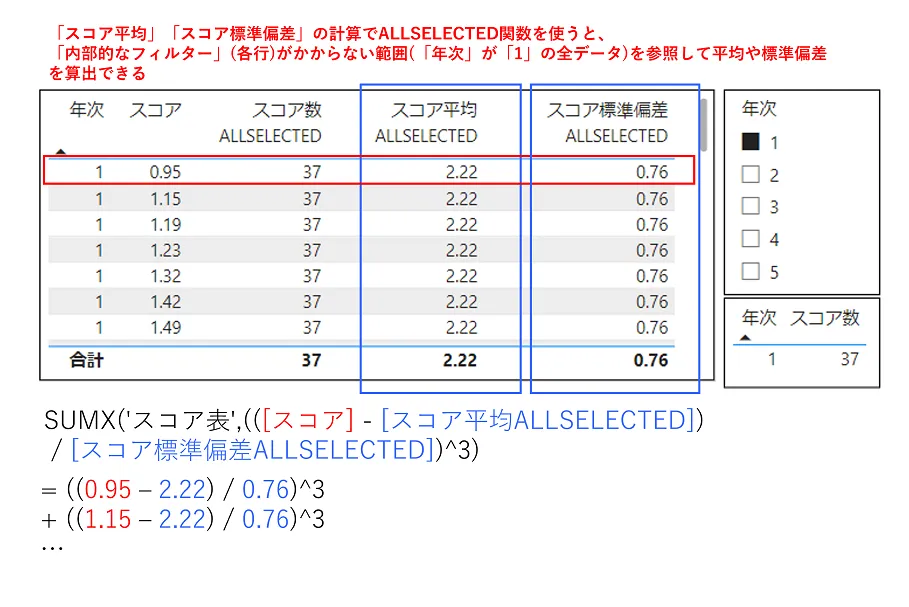
スコア数ALLSELECTED　　　　= COUNTX( ALLSELECTED('スコア表') ,[スコア])  
スコア平均ALLSELECTED　　　= AVERAGEX( ALLSELECTED('スコア表') ,[スコア])  
スコア標準偏差ALLSELECTED　= STDEVX.P( ALLSELECTED('スコア表') ,[スコア])  

これによって、集計対象となるデータ（「年次」が「1」のデータ）全体を参照して計算できるようになりました（図16を参照）。なお、「スコア数ALLSELECTED」は「歪度」の計算には使用しませんが、「スコア平均ALLSELECTED」や「スコア標準偏差ALLSELECTED」で参照しているデータの範囲を示すために便宜上カラムに入れています。

図16では「スコア数ALLSELECTED」の各値がテーブル全体の行数である37になっており、「スコア平均ALLSELECTED」や「スコア標準偏差ALLSELECTED」が37個のスコアの平均および標準偏差を出したものになっています。

そこで出した「スコア平均ALLSELECTED」や「スコア標準偏差ALLSELECTED」を、各「スコア」とあわせて計算することで、「歪度」を正しく算出できるようになりました。
「スコア平均」および「スコア標準偏差」でALLSELECTED関数を使用するように修正した「歪度」の計算式は以下のようになります。

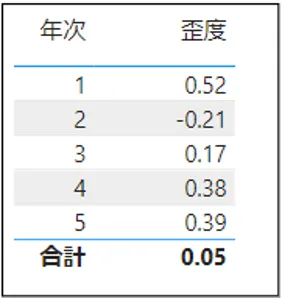
歪度 = [スコア数]/(([スコア数]-1)*([スコア数]-2))*SUMX('スコア表',(([スコア] - [スコア平均ALLSELECTED]) / [スコア標準偏差ALLSELECTED])^3)

この式をもとに「歪度」を算出すると図17のようになり、各「年次」について「歪度」が算出できるようになりました。

まとめ

この記事ではPower BIでのフィルタリングの考え方について、正規分布や歪度のような統計量を計算する場合を例に説明しました。
Power BIでデータ分析をするにあたっては、今回とりあげた「外部的なフィルター」および「内部的なフィルター」のような考え方を正しく理解している必要があります。